Biquadratische Gleichung
Wir lernen heute das Thema Biquadratische Gleichungen!
Sicherlich fragt ihr euch, ob das nicht dasselbe ist wie die Quadratische Gleichung! Antwort: NEIN!
Wir wollen nun einmal erklären was der Unterschied der beiden ist.
Was ist eine Quadratische Gleichung?
Bei einer quadratischen Gleichung kommt die Unbekannte Variable x mindestens einmal in der 2.Potenz vor, aber in keiner höheren Potenz! Außerdem darf noch ein konstantes Glied c (auch Absolutglied genannt) in der Gleichung vorkommen, sowie ein ein lineares Glied. Im Allgemeinen hat eine quadratische Gleichung somit folgende Form: ax2+bx+c=0
Dabei sind a,b und c irgendwelche Zahlen. Beispiel: 5x2+6x+7=0
Natürlich darf der Koeffizient a nicht gleich Null sein, denn dann
würde der erste Summand zu Null, und es würde nur eine lineare
Gleichung vorliegen.
Notiz: (a) ist das Quadratische Gleid, (b) das Lineare Glied und (c) das Konstante!
Was ist die Biquadratische Gleichung?
Eine biquadratische Gleichung ist eine Gleichung 4. Grades, in der nur die 2. und 4. Potenz sowie ein absolutes Glied vorkommen. Sie kann durch die Substitution x² = z in eine quadratische Gleichung umgewandelt und gelöst werden. Ebensfalls enthält die Biquadratische Gleichung keine ungeraden Exponenten! Biquadratische Gleichungen können bis zu vier verschiedene Lösungen haben. Existiert eine Lösung nicht, so wird dies durch das Symbol ◊ ausgedrückt. Es hat die Form
![]()
Die Nullstellen der Biquadratischen Gleichung könnt ihr mit der Formel berechnen.
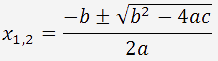
Die Berechnung der Diskriminante einer quadratischen Gleichung lautet

Die Diskriminante kann positiv, gleich Null oder negativ sein:
Nach den inhaltlichen Unterschieden berechnen wir zur Biquadratischen Gleichung einen Beispiel. Diese berechnen wir Schrittweise zum Verständnis
Gegeben haben wir die folgende Gleichung
Wir wissen, dass die Koeffizienten
- a= 1
- b= -8
- c= 16
sind
Wir setzen nun die Werte in die Lösungsformel ein und erhalten dabei;
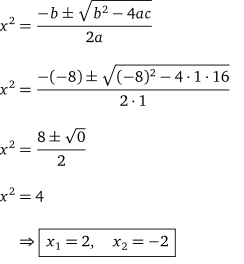
Unser Lernvideo zu : Biquadratische Gleichung
Das gleiche machen wir für das nächste Beispiel ebenfalls. Wir wollen die Biquadratische Gleichung berechnen
6x² – 17x + 12 = 0
Unsere Koeffizienten sind
- a = 6
- b = -17
- c = 12
Nun setzen wir das ganze wieder in die obige Formel ein und erhalten folgende Lösungen
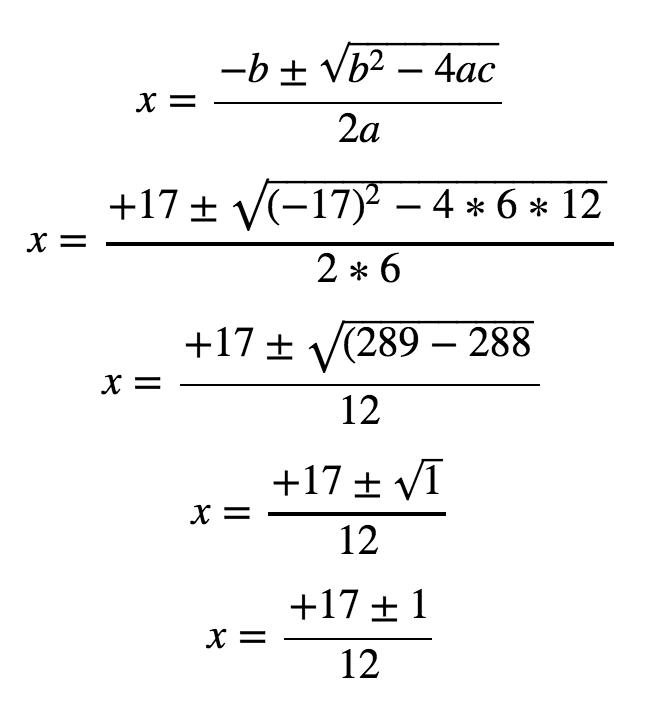
Somit lauten unsere X-Werte
Merke dir folgendes
- Ist a = +1, kann diese Kleine Lösungsformel angewendet werden x² + px + q = 0
Die Diskriminante (p/2)² – q entscheidet über die Anzahl der Lösungen der quadratischen Gleichung
- D > 0 d.f. 2 Lösungen L = {x1; x2} da zwei Schnittpunkte mit der x-Achse
- D = 0 d.f. 1 Lösung L = {x} da ein Berührungspunkt mit der x-Achse
- D < 0 d.f. keine Lösung L = { } da kein Schnittpunkt mit der x-Achse
