Bruchungleichung
Wir befassen uns mit dem Thema Bruchungleichungen!
Tatsächlich gibt es nicht nur unsere linearen Gleichungen, sondern auch Bruchungleichungen. Diese sollten mindestens aus einem Bruchterm bestehen. Wir benötigen zur Lösung von Bruch und Gleichungen die Äquivalenzumformung. In diesem Zusammenhang ist es sinnvoll, auch einen Blick auf diese Rechenverfahren zu werfen.
Was ist der Unterschied zwischen Bruchgleichung und Bruchungleichung?
- Bruchgleichungen lassen sich durch Äquivalenzumformungen lösen. Es gilt: Es darf kein Wert für eine Variable eingesetzt werden, welcher zu einer Division durch Null führt. Zu bestimmen sind also die Nennernullstellen, denn genau diese Werte gehören nicht zur Definitionsmenge.
- Bruchungleichungen lassen durch Äquivalenzumformungen lösen. Zuvor muss jedoch ein Blick auf die Nenner der Bruchungleichungen geworfen werden, um die Definitionsmenge zu bestimmen.Es gilt: Es darf kein Wert für eine Variable eingesetzt werden, welcher zu einer Division durch Null führt. Zu bestimmen sind also die Nennernullstellen, denn genau diese Werte gehören nicht zur Definitionsmenge. Ebenfalls zu beachten ist, dass bei der Multiplikation mit einer negativen Zahl oder bei der Division durch eine negative Zahl das Relationszeichen umgekehrt werden muss. Wird eine Bruchungleichung mit einer Variablen multipliziert oder durch sie dividiert, muss eine Fallunterscheidung gemacht werden.
Den Unterschied haben wir nun erklärt! Eine Bruchungleichung besteht nicht nur aus einem Bruch. Es kann passieren, dass ihr auch Aufgaben mit mehreren Brüchen habt. Auch da haben wir folgende Ansätze um die Aufgabe Erfolgreich zu lösen. Nur man sollte wieder wie folgt einmal die Unterschiede kennen.
Wie du Bruchungleichungen lösen kannst?
Eigentlich bestimmen wir wie bei den Gleichungen zunächst einmal die Definitionsmenge. Im Prinzip ist es möglich, hier alle Werte anzunehmen.
Eine Ausnahme bilden die Werte, die im Nenner 0 ergeben. Wir wissen schon aus der Bruchrechnung, dass wir durch Null niemals dividieren dürfen. Wir haben mit den > < Zeichen zu tun, das ist eigentlich der einzige Unterschied zu den Gleichungen.
Ansonsten unterscheiden sich die einzelnen Verfahren in der Lösung nur unwesentlich. Dennoch wollen wir im Folgenden detaillierter darauf eingehen.
Merke: Bei den Gleichungen betrachten wir den Nenner und den Zähler gesondert.
Bruchungleichungen mit ein oder zwei Brüchen:
(Satz über das Vorzeichen eines Quotienten):
Löse die Ungleichungen, indem du beide Brüche zusammenfasst (auf eine Seite bringen, die Brüche durch Erweitern gleichnamig machen und zusammenfassen) und dann den folgenden Satz anwendest:
- Ein Bruch ist größer als Null, wenn Zähler und Nenner größer als Null sind, oder wenn beide kleiner als Null sind. Ein Bruch ist kleiner als Null, wenn Zähler und Nenner unterschiedliche Vorzeichen haben.
Bruchungleichungen mit zwei oder mehr Brüchen:
(Umformung in die Produktform einer algebraischen Ungleichung) :
- Löse die Ungleichungen, indem du alle Brüche auf eine Seite bringst, die Brüche durch Erweitern gleichnamig machst, die Brüche zusammenfasst und mit dem Quadrat des Nenners multiplizierst.
Wir berechnen gemeinsam einen Bespiel. Folgende Ungleichung haben wir:
![]()
- und addieren die Brüche
![]()
- Beide Seiten der Gleichung haben wir mit dem Hauptnenner (x – 3) multipliziert. Jetzt müssen wir die Fallunterscheidung machen!
Fall 1: x > 3 Faktor ist positiv also kein Vorzeichenwechsel!
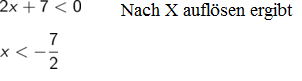
Das ist nicht zu erfüllen für x > 3. Die Lösungsmenge für diesen Fall ist leer L1=Ø
Fall 2: x < 3 Faktor Negativ, Vorzeichenwechsel!
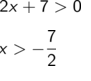
Also ist die Lösungsmenge in diesem Fall
![]()
Zusammengefasst
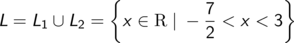
ÜBUNGSAUFGABEN: Bruchungleichungen korrekt lösen
Nun wollen wir an dieser Stelle nicht verbleiben und euch dazu animieren, in die Übungsaufgaben einzusteigen. Nur wenn er täglich trainiert, könnt ihr schon bald Bruchungleichungen ohne Probleme lösen. Ihr dürftet über unsere Schrittfolge bereits erkannt haben, dass Brüche, gemischte Zahlen, Gleichungen und Bruchungleichungen allesamt zusammenhängen. Ein gesundes Basiswissen bildet also ein mathematisches Fundament, das ihr bestenfalls Schritt für Schritt beherrscht.


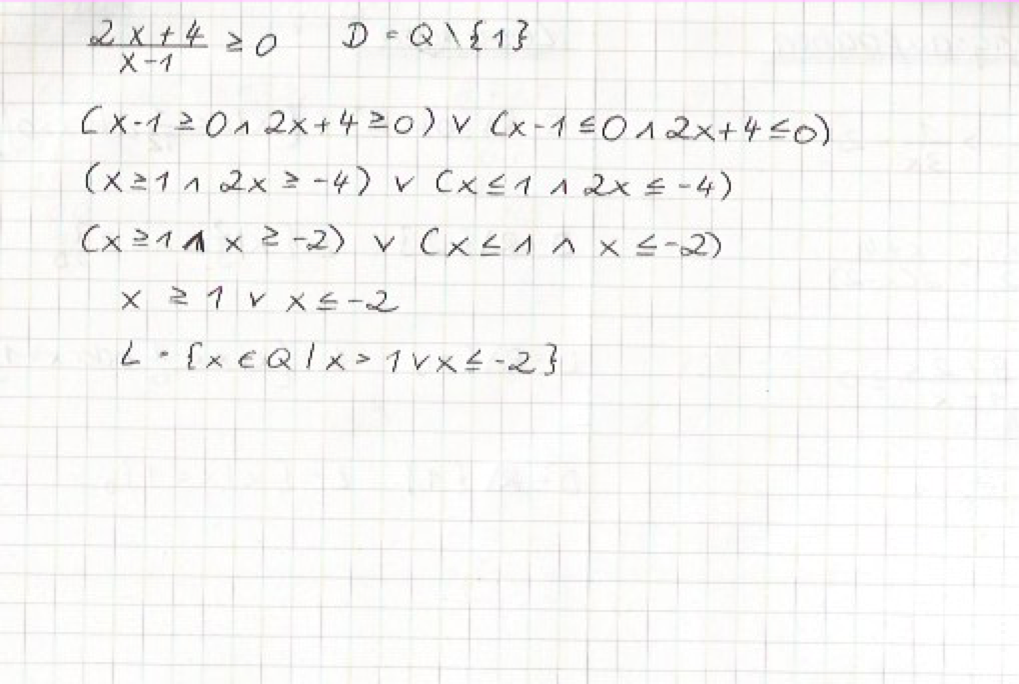
Unser Lernvideo zu : Bruchungleichung
Anderes Beispiel
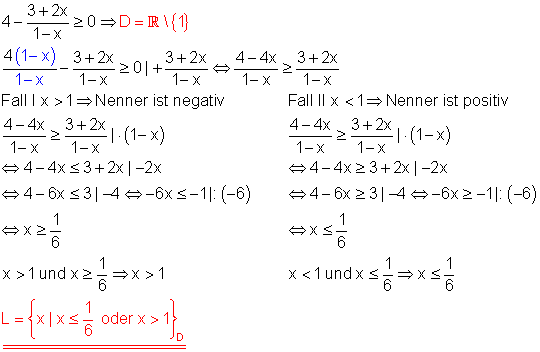
Merkt euch die folgende Vorgehensweise beim Lösen einer Bruchungleichung
- Passt euch die Definitionsmenge der Ungleichung an. Da möglicherweise für manche Zahlen der Nenner in einer Bruchungleichung 0 werden kann, was mathematisch nicht passieren kann, müssen diese Zahlen aus dem Definitionsbereich gestrichen werden. Erst danach kann man mit der Äquivalenzumformung beginnen, da sonst nicht mehr erkennbar ist, welche Zahlen ungültig sind.
- Formt die Bruchungleichung mit Hilfe von Äquivalenzumformungen um, damit auf einer der beiden Seiten nur noch die 0 steht. Falls das Ungleichheitszeichen ein „gleich“ enthält, so löst man zuerst die Gleichheit, als ob es sich um eine normale Gleichung handelt. Wenn im Definitionsbereich die Lösung vorkommt, so gehört diese Lösung auch letztendlich zur Lösungsmenge der Ungleichung
- Zum schluss macht ihr eure Fallunterscheidung. Ein Bruch ist nämlich genau dann größer bzw. kleiner Null, wenn die Vorzeichen von Zähler und Nenner gleich bzw. unterschiedlich sind. Das heißt, dass für jeden Fall zwei Berechnungen gemacht werden müssen. Falls die Bruchungleichung größer als 0 sein soll, so müssen Zähler und Nenner entweder größer oder kleiner Null sein, welches man berechnet und schaut, welcher Fall eintreten kann. Dieser Fall ist dann die Lösung für die Bruchungleichung. Falls der Bruch aber kleiner als 0 sein soll, so müssen die Vorzeichen unterschiedlich sein und man schaut, wann der Zähler positiv und der Nenner negativ ist und umgekehrt. Auch hier wieder die Fallunterscheidung, ob die Fälle eintreten können oder nicht. Der einzutretende Fall ist die Lösungsmenge für die Bruchungleichung.
