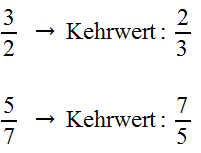Bruchrechnung Grundbegriffe – Erweitern, Kürzen, Kehrwert
Hier erklären wir einige Grundlagen der Bruchrechnung. Wie erweitert oder kürzt man einen Bruch und wie bildet man den Kehrwert.
Unser Lernvideo zu : Bruchrechnung Grundbegriffe – Erweitern, Kürzen, Kehrwert
Erweitern
Um in die Bruchrechnung einsteigen zu können, müssen zunächst einige Grundbegriffe erklärt werden. Oft muss ein Bruch erweitert werden. Dies bedeutet, dass man Zähler und Nenner mit derselben Zahl multipliziert. Dabei bleibt der Wert des Bruchs gleich. Wenn sich dadurch Vorteile ergeben, darf ein Bruch beliebig erweitert werden.
Beispiele
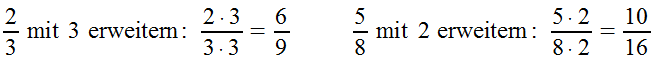
Kürzen
Das Kürzen ist das Gegenteil vom Erweitern. Man dividiert Zähler und Nenner durch den gleichen Wert. Das Ziel dabei ist, den Bruch mit möglichst kleinen Zahlen zu schreiben. Wir benötigen also den größten gemeinsamen Teiler beider Zahlen. Wie man dies berechnet, wurde bereits im Artikel „größter gemeinsamer Teiler“ erklärt. Wenn wir Zähler und Nenner durch den größten gemeinsamen Teiler (ggT) teilen, können wir sicher sein, dass der Bruch nicht weiter kürzbar ist. Der Wert des Bruchs bleibt beim Kürzen derselbe, da wir Zähler und Nenner durch die gleiche Zahl teilen.
Beispiele
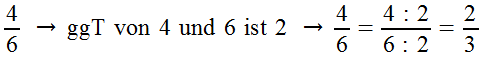
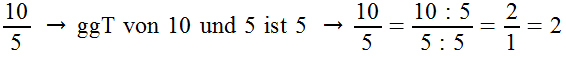
Bei dem zweiten Beispiel gibt es außerdem eine Besonderheit. Wir können das Ergebnis zu 2 vereinfachen, da 2 : 1 = 2 ist. Immer wenn im Nenner eine 1 steht, können wir deshalb den Bruch einfach weglassen und müssen nur den Zähler notieren.
Kehrwert
Den Kehrwert eines Bruches erhält man, indem man Zähler und Nenner vertauscht.
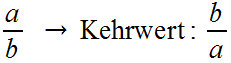
Beispiele