Doppelbruch
Ein Doppelbruch wird auch Mehrfachbruch genannt. Es ist ein Bruch, der selber nochmal geteilt wird. Entweder durch einen weiteren Bruch oder durch eine ganze Zahl. Desweiteren gibt es die Möglichkeit, dass eine ganze Zahl durch einen Bruch geteilt wird, auch dies gehört zu Kategorie des Doppelbruchs.
Zum Verständnis schauen wir uns einen Doppelbruch konkret an:
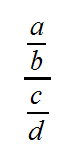
Dieses ist ein allgemeiner Doppelbruch, die jeweiligen Buchstaben a, b, c, d sind Variablen für beliebige natürliche Zahlen. Hier haben wir wie bei einem klassischem Bruch einen Zähler und einen Nennen. Nun ist der Unterschied, dass sowohl im Zähler als auch im Nenner ein Bruch steht.
Unser Lernvideo zu : Doppelbruch
Berechnen eines Doppelbruchs
Das Auflösen eines Doppelbruchs wird mit den bereits bekannten Rechenregeln für Brüche durchgeführt. Wie bereits oben erwähnt, haben wir sowohl im Nenner als auch im Zähler einen Bruch, was überhaupt das Faktum des Doppelbruchs darstellt. Somit kann man auch die beiden Brüche nicht mit einem Bruchstrich, sondern auch mit dem Divisionszeichen darstellen:
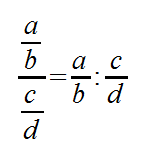
Zur Berechnung dieses Quotienten bedienen wir uns der allgemeinen Regel, die besagt, dass wenn wir durch einen Bruch teilen wollen, mit dem Kehrwert multiplizieren. Somit erhalten wir folgende Rechenschritte:
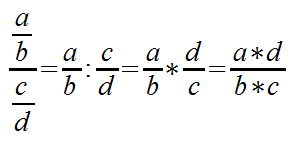
Aus dem Doppelbruch wird zunächst eine anders geschriebene Division. Dann multiplizieren wir mit dem Kehrwert und erhalten die Lösung des Doppelbruches. Wir können uns auch merken, dass der Bruch im Zähler stehen bleibt. Der Bruch im Nenner wird gedreht und der Nenner d wird in den Zähler gesetzt. Und der Zähler c bleibt im Nenner.
Beispiel
![]()
Wir wollen den abgebildeten Bruch lösen. Dazu nutzen wir wie im allgemeinen Beispiel, zunächst den Kehrwert und multiplizieren danach.
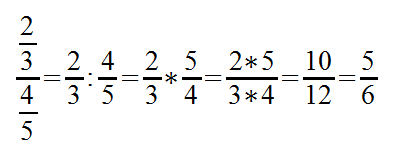
Der Doppelbruch wird zu einer anderen Schreibweise umgeformt, danach mit dem Kehrwert multipliziert. Die Ergebniss des Zählers und des Nenners werden berechnet und noch gekürzt, so dass wir zum Ergebnis kommen.
Nicht vollständiger Doppelbruch
Es besteht auch die Möglichkeit, dass im Zähler oder Nenner, kein Bruch, sondern eine natürliche Zahl stehen. Auch dies fällt unter die Bezeichnung Mehrfachbruch, und wird auf die selbe Weise gelöst.
Beispiel 1
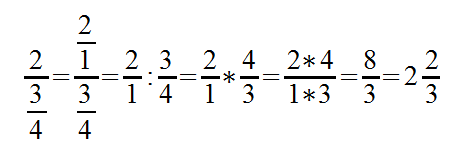
In diesem Doppelbruch haben wir im Zähler die natürliche Zahl 2. Sie wird zu einem Bruch erweitert und danach die selben Schritte vollzogen wie zuvor. Als erstes wird die Division anders notiert, dann mit dem Kehrwert mal genommen und am Ende ein gemischter Bruch notiert.
Diese Berechnung kann man auch mit einer Kurzform notieren:
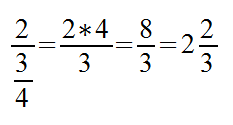
Bei dieser Kurzform nutzen wir das bisherige Wissen. Wir wissen, dass der Zähler des Bruchs im Nenner im Zähler bleibt und der Nenner wir nach dem Kehrwert in den Zähler gesetzt. Wenn wir dieses berücksichigen, können wir uns einige Zwischenschritte sparen.
Beispiel 2
Genau wie im Beispiel ein, betrachten wir nun einen nicht vollständigen Doppelbruch. Nun ist die natürliche Zahl jedoch im Nenner, statt im Zähler:
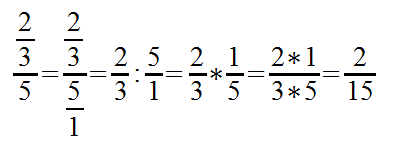
Auch hier ist die Auflösung des Doppelbruchs genau wie zuvor. Der Nenner wird mit einer Eins zum Bruch. Dann wird der Bruch als Division notiert, der Kehrwert berechnet und das Ergebnis notiert. Genau wie beim Beisiel ein, können wir auch hier eine kurze Version nutzen:
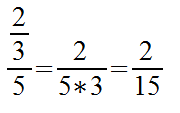
Durch das bisherige Wissen, können wir den Bruch des Zählers aufteilen. Der Zähler 2 bleibt im Zähler und der Nenner 3 wird in den Nenner des Doppelbruchs gesetzt. Das Ergebnis ist das selbe.
Somit haben wir die Brüche und Doppelbrüche kennengelernt. Da das Bruchrechnen oft unterschätzt wird und vor allem leicht vergessen wird, empfehlen wir euch, das Thema ein zweites Mal durch zu sehen, um das Erlernte zu festigen.
