cos x Ableitung
Eigenschaften Cosinusfunktion
►Definitionsberich: D=ℝ
►Wertebereich: W=[−1;1]
►Periode: T=2π
►Symmetrie: achsensymmetrisch zur y-Achse
►Nullstellen: x0=π2+k⋅π , k∈ℤ
►Maxima: max=2k⋅π , k∈ℤ
►Minima: min=(2k+1)⋅π , k∈ℤ
Merke: Der Sinus und der Kosinus haben den gleichen Definitionsbereich und den gleichen Wertebereich. Der Definitionsbereich sind die reellen Zahlen. Der Wertebereich ist das Intervall [-1,1].
Die richtige Regel anwenden
Ihr müsst immer die Kettenregel benutzen. Die Kettenregel braucht man immer dann, wenn man es nicht mehr nur mit den „Grundfunktionen“ zu tun hat, sondern wenn statt des einzelnen x ein erweiterter Ausdruck steht. Schon ein einfaches Minus stellt in diesem Sinne eine Erweiterung dar bsp 2*(cos) → -2(cos)
►Bei der Kettenregel wird die äußere Funktion zuerst abgeleitet und mit der inneren Ableitung multipliziert.
Wir schauen uns eine Cosinusfunktion mal an. So sieht eine Cosinusfunktion aus
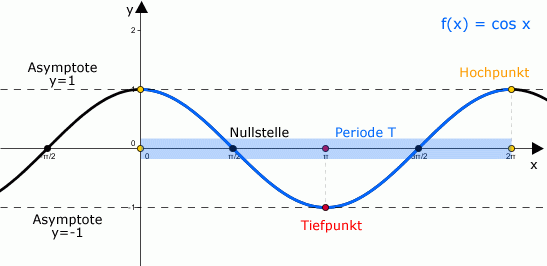
►Man erkennt, dass sich die Funktion in regelmäßigen Abständen wiederholt, deswegen nennt man die Kosinusfunktion auch periodisch. Der Abstand zwischen zwei Wiederholungen nennt man die kleinste Periode T.
Die Kettenregel Formel
![]()
- g(x) = äußere Funktion
- g′(x) = äußere Ableitung
- h(x) = innere Funktion
- h′(x) = innere Ableitung.
Ganz wichtig ist besonders das Ableiten von Cosinus. Im Gegensatz zu Zahlen werden Cosinus und Sinus wie in einem Kreis abgeleitet, dass sich ständig widerholt. An diesem Muster könnt ihr euch halten. Am besten ist es, wenn ich das Schema auswendig lernt. Denn dann kann nichts schief gehen
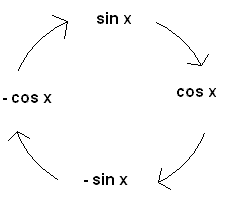
Beispiele
f(x) cos(0,5x-1) ► f`(x)= -0,5sin (0,5x-1)
f(x)= cos(2x) ►f`(x)= -2sin(2x)
f(x)= cos(x2+x) ►f`(x)= -sin(x2+x)*(2x+1)
