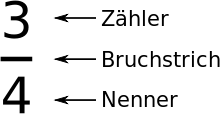
Definitionsbereich bei Brüchen
Warum ist Definitionsmenge wichtig?
- In der Regel wird vor dem Lösen der Bruchgleichung der Definitionsbereich (oder die Definitionsmenge) der Bruchgleichung bestimmt.
- Wenn man später die Gleichung gelöst und ein Ergebnis erhalten hat, muss man nachprüfen, ob es überhaupt im Definitionsbereich liegt. Wenn es nicht darin enthalten ist, ist es nicht Lösung der Gleichung, auch wenn man ansonsten richtig gerechnet hat.
► Der Definitionsbereich wird in der Mengenschreibweise i.d.R. mit einem D in Blockschrift angegeben: ⅅ.
Mathematische Schreibweise
Um Zahlen aus der Grundmenge auszuschließen, verwendet man das Mengenoperationszeichen ∖∖ (also einen nach rückwärts gekippten Strich).
- „∖∖“ bedeutet „ohne“.
- Danach kommen die ausgeschlossenen Zahlen.
- Um diese Zahlen herum steht eine Mengenklammer: „{…}{…}“
Einige Beispiele
- Das Format für den Definitionsbereich ist eine linke Klammer, dann Anfangs- und Endpunkt des Definitionsbereiches getrennt durch ein Komma und dann eine rechte Klammer.
- Zum Beispiel [-1,5). Das bedeutet der Definitionsbereich geht von -1 bis 5.
Benutze eckige Klammern,[und], falls die Zahl zum Definitionsbereich gehört.
- Beispiel [-1,5) ist -1 im Definitionsbereich enthalten.
- Benutze runde Klammern,(und), falls die Zahl nicht zum Definitionsbereich gehört.
- Im Beispiel [-1,5) gehört 5 nicht zum Definitionsbereich. Der Definitionsbereich geht beliebig nahe an 5 heran, d.h. 4.999…
- Benutze “U” (das heißt „Vereinigung“) um Teile des Definitionsbereiches, die durch Lücken getrennt sind, zu verbinden.‘
- Zum Beispiel [-1,5) U (5,10]. Das heißt dass der Definitionsbereich von -1 bis 10 inklusive geht, aber dass es eine Definitionslücke bei 5 gibt. Das kann vorkommen wenn eine Funktion zum Beispiel “x – 5” im Nenner stehen hat.
- Du kannst so viele „U“-Symbole wie nötig verwenden, wenn der Definitionsbereich mehrere Lücken hat.
- Benutze das „Unendlich“-Zeichen (mit + oder -) um auszudrücken, dass der Definitionsbereich in dieser Richtung unendlich weiter geht.
- Benutze immer ( ) und nicht [ ], wenn du das Unendlich-Symbol verwendest.
Unser Lernvideo zu : Definitionsbereich bei Brüchen
Vorgehensweise zum Bestimmen der Definitionsmenge
- Für jeden der vorkommenden Brüche
- schreibt man den Nenner heraus
- setzt ihn gleich 0
- und löst nach der Variablen auf.
Alle Zahlen, die man dabei als Lösungen erhält, muss man bei der Definitionsmenge ausschließen:
- Man schreibt die Grundmenge hin (meist Q oder R),
- dann ∖∖
und dann in Mengenklammern all die Zahlen, für die irgendein Nenner Null werden würde.
Beispiel
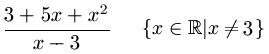
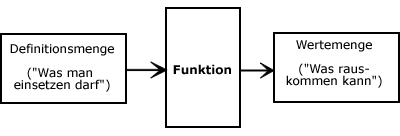
Bei diesem Bruch darf man für „x“ die Zahl 3 nicht einsetzen. Für „x“ = 3 wäre der Nenner sonst x – 3 = 3 – 3 = 0. Und durch Null darf nicht dividiert werden
oder
![]()
Würden wir für „x“ die Zahl 0 einsetzen, dann würde man bei diesem Bruch durch Null dividieren. Und das darf man eben nicht. Die Schreibweise rechts davon besagt nun, dass man für x die Zahl 0 nicht einsetzen darf.
weitere folgende Beispiele

Der Bruchterm ist für x = 3 nicht definiert.Der Term -2 ist auf ganz ℚ definiert.
Die beiden Bruchterme sind also für alle x ∈ ℚ {3} definiert und äquivalent.
Merke
►Die „verbotene“ Zahl erkennt man sofort
►oder man erhält sie durch Nebenrechnung
►Nenner gleich Null setzen
Wenn immer noch Probleme dabei hast merke dir die Eselsbrücke
0:5 geht ► 0€ aufteilen auf 5 Leute. Jeder kriegt 0€
5:0 geht nicht ► 5€ auf 0 Personen aufteilen? Man kann nicht sagen, was da raus kommt
Woraus Besteht noch einmal ein Bruch?