Die Verschiebung in y-Richtung
Um eine quadratische Funktion in y-Richtung zu verschieben müssen wir einfach den gewünschten Wert addieren oder subtrahieren. Wenn wir zum Beispiel zu der Funktionsvorschrift zwei addieren, erreichen wir, dass der y-Wert an allen Punkten um 2 erhöht wird. Wir haben die Funktion also um zwei nach oben verschoben. Wenn wir hingegen etwas abziehen würden, würde die Funktion nach unten verschoben werden.
Unser Lernvideo zu : Die Verschiebung in y-Richtung
Beispiel
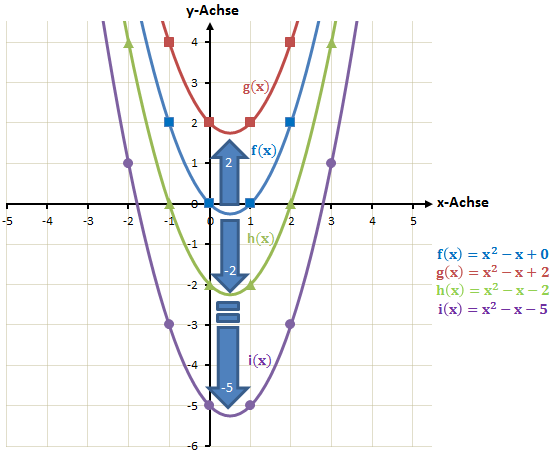
Genauso funktioniert es übrigens auch bei der Scheitelpunktform. Natürlich verschiebt sich durch die Verschiebung auch der Scheitelpunkt und der y-Achsenabschnitt nach unten oder oben.
Interessante Fragen und Antworten zu Die Verschiebung in y-Richtung
Wie behalte ich den y-Achsenabschnitt bei und wechsle nur den x-Achsenabschnitt? |
| Wie behalte ich den y-Achsenabschnitt bei und wechsle nur den x-Achsenabschnitt Zwei dimensionale Graphen haben stets eine horizontale Achse, diese wird auch als x-Achse bezeichnet und eine vertikale Achse, die y-Achse. Die Stellen, welche die Achsen schneidet, sind die Achsenabschnitte, wo sich die repräsentierten Werte der Kurve befinden. An dem y-Achsenabschnitt schneidet sich die Kurve der y-Achse.Dementsprechend handelt es sich bei der x-Kurve um den x-Achsenabschnitt. Eine Bestimmung oder ein Wechsel dieser x-Achse kann einfach möglich sein oder es ist ein komplizierter Vorgang. Die akribische Bestimmung richtet sich dabei immer nach der Gleichung für die Kurve. So könnte der y-Achsenabschnitt bestimmt werden, wenn bei einer einfachen Gleichung mit zwei Variablen eine Null für das x anstatt für y eingesetzt wird. Y-Achsenabschnitt bestimmenBei linearen Funktionen ist der y-Achsenabschnitt der Wert, wo sich Funktionsgraph und y-Achse schneiden. Deshalb sollte der y-Achsenabschnitt immer zuerst ermittelt werden. Dabei gilt die Funktionsvorschrift: y = mx + b. B wird dabei als y-Achsenabschnitt wirksam. Ist der Funktionswert der y-Achse abgelesen (y-Achsenabschnitt), folgt das Einsetzen des x-Wertes zur Lösung und Ermittlung der Gleichung. Liegt der Punkt auf der y-Achse und schneidet die x-Achse im Koordinatenursprung, liegt x bei Null. So kann anschließend bei der Gleichung das x=0 sein. Also ist der y-Wert bestimmt und der x-Achsenabschnitt kann weiter verschoben werden, wobei der y-Achsenabschnitt beibehalten wird. |
Wie kann ich den y-Achsenabschnitt immer direkt in der Funktion ablesen ohne zu Rechnen? |
| Der y-Achsenabschnitt wird auch Ordinatenabschnitt beziehungsweisea Interzept gennant. Bei einer einer linearen Funktion nimmt er den Wert an, an dem der Graph der Funktion die y-Achse schneidet.Neben der rein rechnerischen Bestimmung kann der y-Achsenabschnitt im Graphen der Funktion abgelesen werden.Ohne Rechnen zu müssen kann man den y-Abschnitt im gezeichneten Graphen ablesen. Wenn eine Zeichnung des Graphen der Funktion gegeben ist, orientiert man sich zunächst an der Stelle Null der x-Achse. Nun befindet man sich praktisch an der Stelle, an der sich die x-Achse sowie die y-Achse kreuzen. Man wirft einen Blick auf den gesamten Graphen der Funktion und macht sich auf die Suche, an welcher Stelle der Graph die y-Achse schneidet. Dies ist entweder überhalb oder unterhalb der x-Achse der Fall. Wenn man den Schnittpunkt der Funktion mit der y-Achse oberhalb der x-Achse entdeckt, befindet man sich im positiven Bereich. Unterhalb der x-Achse befindet man sich im negativen Bereich. Wenn die Entfernung des Schnittpunkts mit bloßem Auge genau identifizierbar ist, benötigt man nicht einmal ein Geodreieck. Ansonsten kann es hilfreich sein, das Geodreieck einzusetzen, um den Wert auf den genauen Milimeterbereich bestimmen zu können. Wichtig ist, dass man bei der Angabe des y-Abschnitt nicht das Vorzeichen vergisst. |
