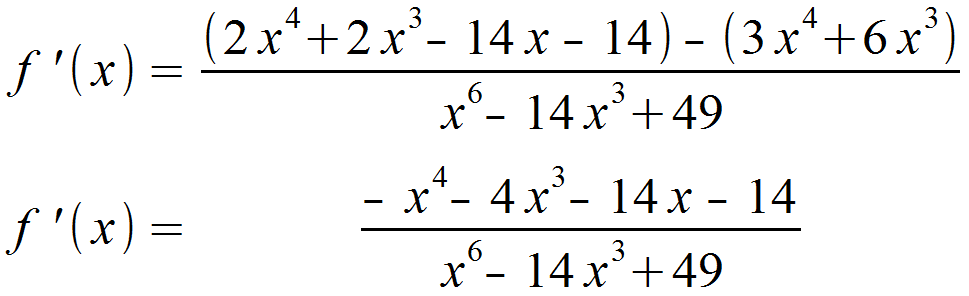Quotientenregel zum Ableiten
Handelt es sich bei der vorliegenden Funktion um einen Bruch, bei dem sowohl im Zähler als auch im Nenner eine Abhängigkeit von x vorliegt, ist für die Ableitung die Quotientenregel anzuwenden. Hierbei werden Zähler und Nenner als einzelne Funktionen betrachtet.
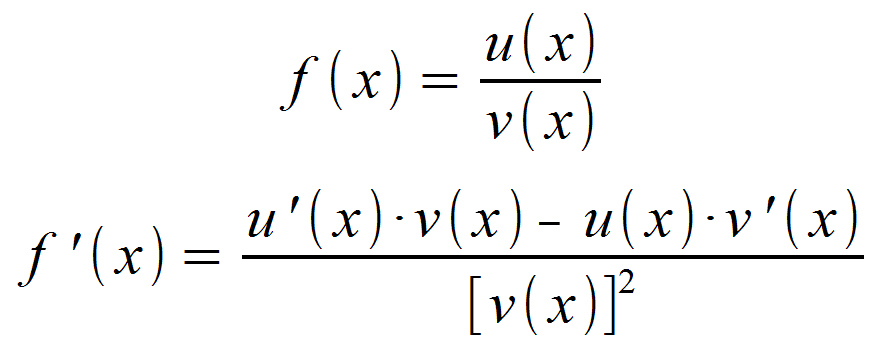
Ähnlich der Produktregel geht man folgendermaßen vor:
- u (x) und v (x) identifizieren
- u ‚(x) und v ‚(x) bilden
- in Formel für f ‚(x) einsetzen
- ausmultiplizieren und vereinfachen
Unser Lernvideo zu : Quotientenregel zum Ableiten
Beispiel
Die folgende Funktion soll abgeleitet werden.
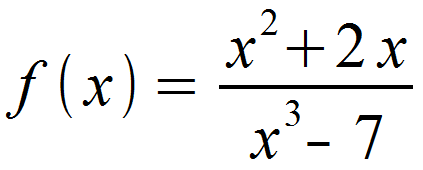
Wir identifizieren zunächst u (x) und v (x).
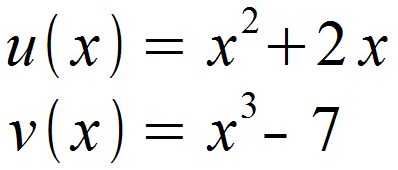
Daraufhin leiten wir diese ab.
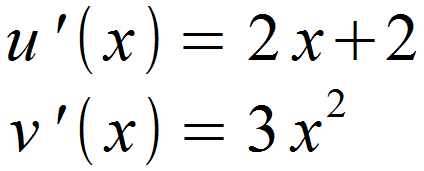
Im nächsten Schritt werden die erhaltenen Funktionen in die Formel für f ‚(x) eingesetzt.
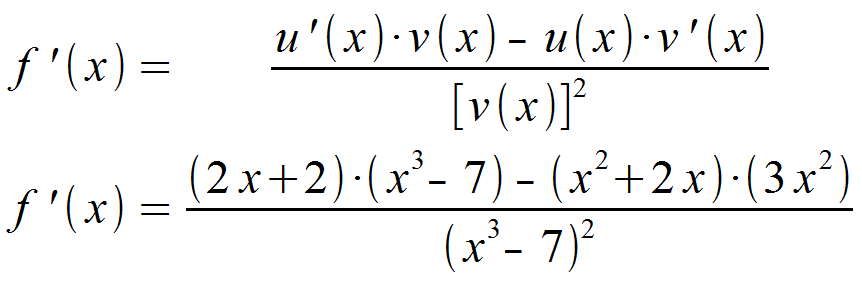
Wir multiplieren aus und vereinfachen abschließend.
(Hinweis: Beim Nenner wurde die 2. Binomische Formel verwendet.)