Differentiationsregeln
Die Notation
Die Ableitung einer Funktion wird mit einem Strich ( ` ) nach der Bezeichnung der Funktion gekennzeichnet. Bei höheren Ableitungen fügt man weitere Striche hinzu. Der Übersichtlichkeit halber verwendet man ab der vierten Ableitung statt der jeweiligen Anzahl an Strichen die entsprechende Zahl hochgestellt und eingeklammert.
►Funktion f(x)
►1.Ableitung f`(x)
►2.Ableitung f„(x)
…
…
► n-te Ableitung f(n)(x)
Differentiationsregeln im Überblick
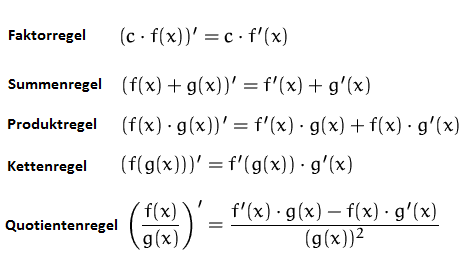
Faktorregel
Faktorregel erlaubt es, konstante Terme vor die Ableitung zu faktorisieren. Dies betrifft nicht nur Zahlen, sondern auch Variablen, die nicht differenziert werden.
![]()
Beispiele
f(x)= 3x2 ⇒ f`(x)= 3*(2*x2-1) ⇒6x
f(x)=-4x4 ⇒ f`(x)= -4*(4*x4-1) ⇒-16x3
Jeder Faktor ohne x bleibt beim Ableiten Erhalten. D.h. du kannst jeden Faktor, der kein x enthält, also von x unabhängig ist einfach abschreiben und musst nur den Rest ableiten. Das bedeutet: Die Faktorregel wird verwendet, wenn eine konstante Zahl mit einer regulären Funktion multipliziert wird.
Summenregel
Die Ableitung von der Summe von Funktionen ist die Summe ihrer Ableitungen.
![]()
Beispiel
- f(x)= e5x+4*e3x
- f`(x)=5e5x+ 12e3x →Ableitung
♦Besteht eine Funktion aus mehreren Termen, so werden diese als einzelne Funktionen betrachtet und können auch einzeln abgeleitet werden.
♦Summenregel besagt, dass die Summe aus zwei differenzierbaren Funktionen wieder differenzierbar ist und dass eine solche Summe aus Funktionen gliedweise differenziert werden kann.
Produktregel
Die Produktregel wird nur benutzt, wenn zwei Funktionen miteinander multipliziert werden. Man verwendet sie immer dann, wenn eine Funktion in der Form „Term mit x“ mal „Term mit x“ vorliegt.
![]()
Vorgehensweise:
- u (x) und v (x) bestimmen
- u ‚(x) und v ‚(x) bilden
- in Formel für f ‚(x) einsetzen
- ausmultiplizieren und vereinfachen
Beispiel
f(x)= 2x3*7x2
u(x)= 2x3 ⇒ abgeleitet u`(x)= 6x2
v(x)= 7x2 ⇒ abgeleitet v`(x)= 14x
f`(x)= 6x2* 7x22x3 *14x ► 42x4+28x4= 70x4 Ableitung!
Kettenregel
Die Kettenregel musst du immer dann anwenden, sobald x in einer Klammer steht und die Klammer eine Hochzahl hat.
![]()
Vorgehensweise:
- u (x) und v (x) bestimmen
- u ‚(x) und v ‚(x) bilden
- in die Formel einsetzen
- ggf. ausmultiplizieren und vereinfachen
♦Bei der äußeren Ableitung wird das betrachtet, was außerhalb der Klammer bei f(x) steht
♦Bei der inneren Ableitung, wird das betrachtet, was innerhalb der Klammer bei f(x) steht
♦Danach wird die innere Ableitung mit der äußeren Ableitung multipliziert
Beispiel
f(x)= -cos(4x)
Äußere Funktion: -cos
Innere Funktion: 4x
Ableitung äußere Funktion : sin
Ableitung innere Funktion : 4
Zusammengefasst: 4*sin(4x)
Quotientenregel
Ein Quotientenregel wird immer dann benutzt, wenn sowohl im Zähler als auch im Nenner einer Funktion ein x vorkommt.
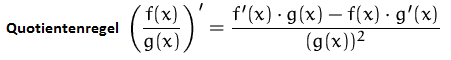
♦Die quotientenregel verwendet man immer bei gebrochenrationalen funktionen.
♦Die Quotientenregel ist eine kombination aus Produkt und Kettenregel
♦Beachte. dass v(x) im Nenner steht. Und was im Nenner steht, darf nicht Null sein. Durch Null darf dich nicht dividiert werden!
Beispiel
f(x)= x2/x
f(x)` = 2x*2-x2*1 / x2
f(x)`= 2x2-x2 / x2
f(x)`= x2/x2
f(x)`=1 Lösung!
