Konstruktion des Thaleskreises
Nun wollen wir den Thaleskreis zeichnen lernen.
Dies geht auf zwei verschiedene Art und Weisen. Zum einen können wir ein Dreieck gegeben haben und erfahren wollen, ob dieses rechtwinklig ist ohne einen Winkel zu messen. Und zum anderen wollen wir mit einem Thaleskreis ein rechtwinkliges Dreieck konstruieren.
Prüfen der Rechtwinkligkeit
Um zu erfahren, ob ein gegebenen Dreieck rechtwinklig ist, können wir den Thaleskreis nutzen.
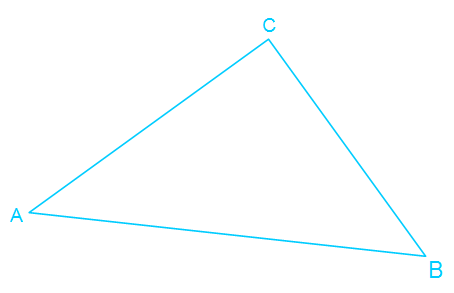
Wir haben ein allgemeines Dreieck ABC. Nun brauchen wir zunächst den Mittelpunkt der längsten Seite AB, um darum einen Kreis zeichnen zu können. Die Ermittlung des Mittelpunkts einer Seite haben wir bereits im Thema Seitenhalbierende oder Mittelsenkrechte auf unserer Homepage bearbeitet. Dies könnt ihr euch im Zweifel gerne noch einmal ansehen.
Wenn wir den Mittelpunkt ermittelt haben, ziehen wir einen Kreis um dieses mit dem Abstand zu A oder B. somit ist die Strecke AB, dann unser Durchmesser.
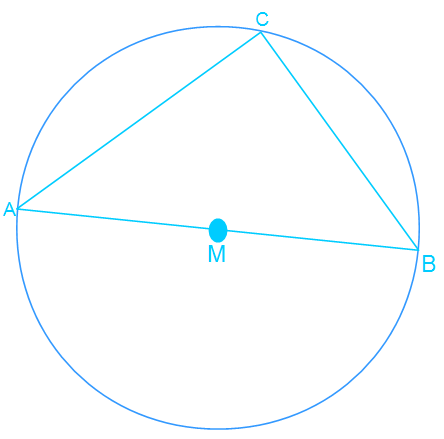
Als letzes überprüfen wir, ob der Punkt C auf dem Kreis liegt. Dieses ist der Fall und Somit haben wir ein rechtwinkliges Dreieck erkannt.
Wenn der Punkt C nicht auf dem Kreis liegen würde, wäre dieses auch kein rechwinkliges Dreieck.
Unser Lernvideo zu : Konstruktion des Thaleskreises
Konstruktrion eines rechtwinkligen Dreiecks
Um ein rechtwinkliges Dreieck zu Konstruieren können wir auch hier den Thaleskreis nutzen, da wir bereits bewiesen haben, dass alle Punkte auf dem Kreis zu einem rechtwinkligen Dreieck führen.
1. Schritt: Wir zeichnen einen Kreis mit einem unbestimmten Radius um einen Punkt M
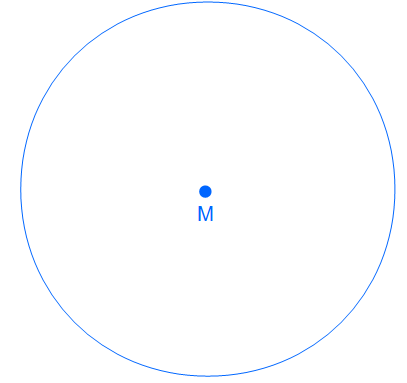
Nun haben wir einen Kreis gezeichnet. Als nächstes zeichnen wir einen Linie ein, die durch den Mittelpunkt M läuft. Dieses ist usner Durchmesser.
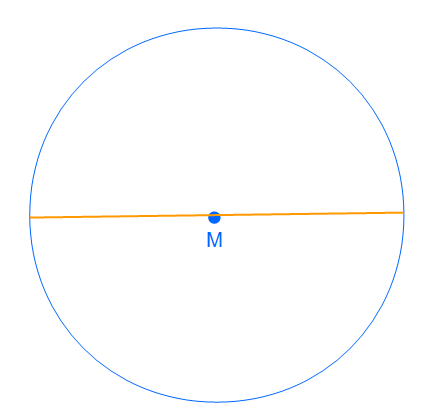
Wir haben nun den Durchmesser gezeichet. Nun können wir jeden beliebigen Punkt auf dem Kreis auswählen und wenn wir ihn mit den Endpunkten des Durchmessers verbinden erhalten wir ein rechtwinkliges Dreieck.
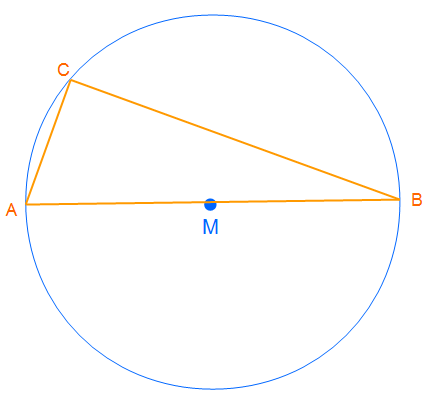
So haben wir ein Dreieck mit einem rechten Winkel in Punkt C konstruiert.
Wenn die Länge der Seite AB bekannt ist, könnt ihr natürlich dieses als Grundlage nutzen. Oft ist auch ein Winkel bekannt, so dass dieses noch bestimmter konstruiert werden kann.
Interessante Fragen und Antworten zu Konstruktion des Thaleskreises
Für was kann man den Thaleskreis/satz des Thales alles verwenden? |
| Der Thaleskreis findet vor allem in der Geometrie Anwendung. Mit ihm ist es möglich, ohne Winkelangabe und ohne Geodreieck ein rechtwinkliges Dreieck zu konstruieren. Hierbei stellt die Hypotenuse gleichzeitig den Durchmesser des Thaleskreises dar. Jeder beliebige Punkt, der nun auf dem Halbkreis über oder unter der Hypotenuse liegt, stellt einen Eckpunkt des rechtwinkligen Dreiecks dar.Außerdem lassen sich mit dem Satz des Thales die Tangenten eines Kreises konstruieren, die durch einen Punkt außerhalb dieses Kreises verlaufen. Dabei stellt die Strecke vom Kreismittelpunkt zum außenliegenden Punkt die Hypotenuse eines rechtwinkligen Dreiecks und damit den Durchmesser des Thaleskreises dar. Der dritte Eckpunkt des rechtwinkligen Dreiecks liegt auf dem Schnittpunkt der beiden Kreise. Er ist der Berührpunkt der Tangente und kommt auf beiden Seiten der Hypotenuse vor. Auf ähnliche Weise lässt sich außerdem ein Rechteck quadrieren. In der fortgeschrittenen Mathematik wird der Satz des Thales auch genutzt, um reelle Quadratwurzeln zu konstruieren. Hierbei wird der Höhensatz oder der Kathetensatz des Euklid zur Hilfe genommen. |
Wie konstruiert man in der Mathematik einen Thaleskreis? |
| Um einen Thaleskreis zu konstruieren, braucht man zunächst eine Linie. Auf dieser Linie werden zwei Endpunkte festgelegt. Diese werden als A und B bezeichnet. Dann wird der Mittelpunkt M dieser Strecke bestimmt. M ist dabei gleichzeitig auch der Mittelpunkt und die Strecke AB ist der Durchmesser des Thaleskreises. Demnach ist die Strecke von Punkt A zu M der Radius des Kreises.Sind diese drei Punkte bestimmt, sticht man mit dem Zirkel in den Mittelpunkt und zeichnet einen Kreis durch die Punkte A und B. Dies ist nun der Thaleskreis. Jetzt kommt der Satz des Thales zum Einsatz. Zeichnet man ein Dreieck in diesen Kreis ein, erhält man immer ein rechtwinkliges Dreieck. Der rechte Winkel befindet sich dabei immer direkt gegenüber der Linie von A bis B, die am Anfang konstruiert wurde. Mit dem Satz des Thales ist es also möglich ein rechtwinkliges Dreieck zu zeichnen, ohne dass man ein Geodreieck benutzen muss. |
