Seitenhalbierende
Die Seitenhalbierende eines Dreiecks ist die Strecke zwischen einem Eckpunkt und dem Mittelpunkt der gegenüberliegeneden Seite.
Unser Lernvideo zu : Seitenhalbierende
In jedem Dreieck gibt es drei Seitenhalbierende. Wenn man alle Seitenhalbierende eines Dreiecks zeichnet, treffen sie sich in einem Punkt, dem Schwerpunkt S.
Die Seitenhalbierende sind gehört zu den sogenannten Transversalen, sie schneiden das Dreieck.
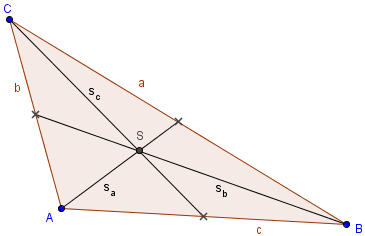
An diesem Dreieck sehen wir alle eingezeichneten Seitenhalbierenden. So ist Sc, die Seitenhalbierende des Eckpunkts C und der Seite c. Sa, die Seitenhalbierende vo Punkt A und der Seite a und natürlich gehört Sb zum Punkt B und der Seite b.
Der eingezeichnete Punkt S, ist der Schwerpunkt dieses Dreiecks. Der Schwerpunkt ist bei einfachen geometrischen Figuren leicht zu ermitteln, aber wie in diesem Beispiel nicht immer ganz so leicht.
Der Schwerpunkt ist der Punkt der Figur, der auch dem Massenmittelpunkt entspricht. Das bedeutet: an diesem Punkt kann man das Dreieck balancieren. Es ist nur wichtig, dass es einheitlich aus demselben Material besteht. Diesen Mittelpunkt kann man natürlich auch durch klassisches „Probieren“ herausfinden. Mathematisch verwenden wir dazu die Seitenhalbierenden.
Zeichnen einer Seitenhalbierenen
Wir gehen nun Schritt für Schritt durch, wie man eine Seitenhalbierende zeichnet.
1. Schritt:
Als erstes zeichnen wir unser Dreieck und beschriften es.
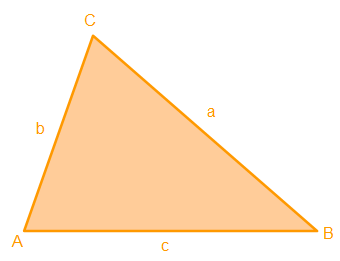
2. Schritt:
Als erstes zeichnen wir die Seitenhalbierende von dem Punkt C und der Seite c. Dazu müssen wir als erstes die Mittelsenktrechte der Seite c einzeichnen, weil eine Seitenhalbierende durch die Mitte der Seite verläuft.
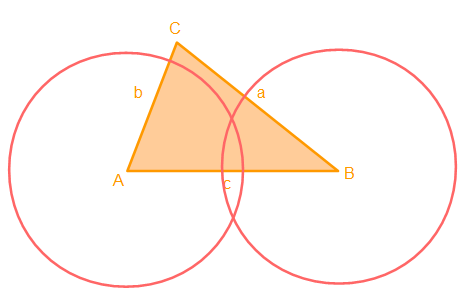
Für die Mittelsenkrechte zeichnen wir mit einem Zirkel zwei Kreise mit dem selben Radius. Einen um den Punkt A und einen um den Punkt B. Der Radius muss so groß sein, dass sich die Kreise zweimal schneiden.
3. Schritt:
Um die Mittelsenkrechte zu vollenden, zeichnen wir nun eine Gerade durch die beiden Schnittpunkte der Kreise. Dann erhalten wir die Mittelsenkrechte der Seite c.
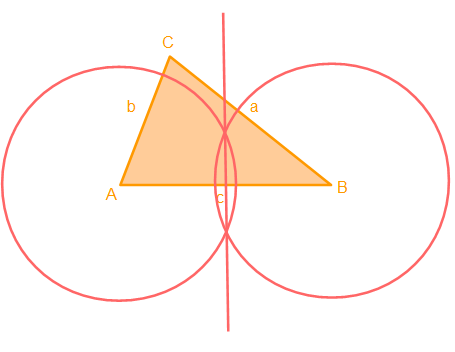
Nun haben wir die Mittelsenkrechte vollendet und zur Übersicht lassen wir hier hier einmal die Kreise weg:
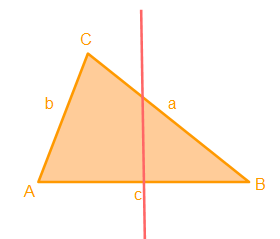
4. Schritt:
Mit der Mittelsenkrechten haben wir den Mittelpunkt der Seite c ermittelt. Wir wissen, die Seitenhalbierende verläuft vom Punkt C zur Mitte der Seite c. Somit können wir nun eine den eben ermittelten Mittelpunkt der Seite c mit dem Eckpunkt verbinden.
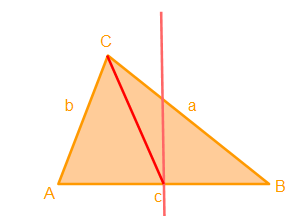
Nun haben wir die Seitenhalbierende Sc ermittelt!
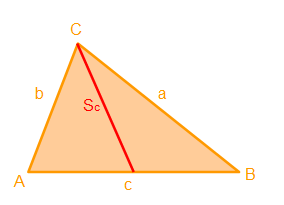
Eine Seitenhalbierende teilt ein Dreieck in zwei kleinere Dreiecke. Die beiden kleineren Dreiecke haben dieselbe Grundfläche und dieselbe Höhe und damit auch denselben Flächeninhalt. Dies kann man für einige Aufgaben nutzen.
Nun haben wir eine Seitenhalbierende gezeichnet. Die beiden anderen Sa und Sb werden auf die selbe Art und Weise gezeichnet, nur muss man die jeweiligen Mittelsenkrechten zur dazu gehörigen Seite zeichnen.
