Antiproportionaler Dreisatz
Den antiproportionalen (umgekehrten) Dreisatz benötigt man für das Rechnen mit antiproportionalen Zuordnung.
Unser Lernvideo zu : Antiproportionaler Dreisatz
Für das Lösen von antiproportionalen Zuordnungen benötigen wir eine Abwandlung des normalen Dreisatzes. Man nennt diese den umgekehrten Dreisatz. Dieser funktioniert ähnlich wie der normale Dreisatz. Vom Vorgehen her ändert sich allerdings eine entscheidende Sache.
Während wir bei dem normalen Dreisatz immer beide Seiten mit demselben Wert Multiplizieren bzw. Dividieren mussten, müssen wir nun beide Seiten immer gegenteilig behandeln. Wenn wir auf der einen Seite multiplizieren, müssen wir auf der anderen Seite dividieren. Wir beschreiben zunächst das Vorgehen allgemein:
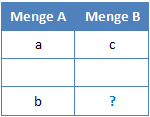
Wieder notieren wir als Erstes links zwischen den beiden bekannten Werten die 1. Um links auf die 1 zu kommen müssen wir durch a teilen. Rechts müssen wir also mit a multiplizieren. Im zweiten Schritt müssen wir links mit b multiplizieren. Für die rechte Seite bedeutet das, dass wir durch b dividieren müssen.
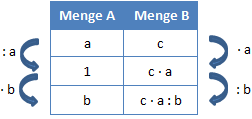
Die linke Seite sieht also genauso aus wie beim normalen Dreisatz. Nur die rechte Seite hat sich geändert.
Beispiel
Um einen großen Erdhaufen abzutragen brauchen 4 Bagger 10 Stunden. Wie lange brauchen 5 Bagger?
Um diese Aufgabe zu lösen, notieren wir zunächst die bekannten Werte. Wir haben auf der einen Seite die benötigten Stunden und auf der anderen Seite die Anzahl der Bagger. Da wir zwei Werte auf der Seite der benötigten Bagger haben, schreiben wir diese Spalte nach links.
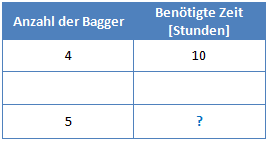
Links müssen wir nun als nächstes die 1 in der Mitte notieren. Wir wollen also berechnen wie lange 1 Bagger brauchen würde. Links müssen wir dazu durch 4 teilen. Rechts müssen wir mit 4 multiplizieren (1 Bagger braucht natürlich mehr Zeit um den Erdhaufen abzutragen als 4).
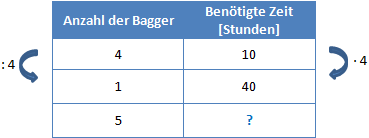
Um nun auf die Zeit zu kommen die 5 Bagger benötigen, müssen wir links mit 5 multiplizieren (sonst kommen wir links nicht auf den Wert 5) und rechts dementsprechend durch 5 teilen.
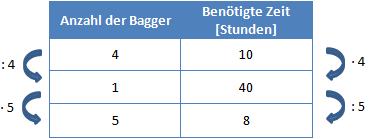
Fünf Bagger müssen also 8 Stunden arbeiten um den Erdhaufen abzutragen.
Antiproportionaler Dreisatz – umgekehrter Dreisatz
Neben dem gewöhnlichen Dreisatz existiert zusätzlich der umgekehrte oder antiproportionale Dreisatz. Dieses mathematische Verfahren dient in der Regel dazu, mit drei gegebenen Werten den Vierten im selben Verhältnis zu ermitteln. Beim umgekehrten Dreisatz rechnet der Anwender mit antiproportionalen Zuordnungen. Wie der Rechenvorgang zu bewältigen und worauf besonders zu achten ist, erfährt der Leser in diesem Artikel.
Dreisatzrechnung – antiproportionale Zuordnung
Für das Berechnen von antiproportionalen Zuordnungen ist es notwendig, zu wissen, was sie bedeuten. Eine Zuordnung ist antiproportional oder umgekehrt, wenn das Doppelte oder das Vierfache einer Größe, die Hälfte oder ein Viertel der zweiten Größe entspricht. Für diese Zuordnungen gilt: „Mehr x bedeutet weniger y“ oder „weniger x bedeutet weniger y“.
Für die Berechnung des umgekehrten Dreisatzes ist eine ähnliche Vorgehensweise wie beim normalen Dreisatz erforderlich. Allerdings ändert sich besonders ein Schritt, der dieses mathematische Verfahren unterscheidet. Beim normalen Dreisatz multipliziert oder dividiert der Anwender beide Seiten mit demselben Faktor. Beim antiproportionalen Dreisatz ist es wichtig, die Seiten gegenteilig zu berechnen. Multipliziert der Mathematiker eine Seite, dividiert er die andere mit dem gleichen Wert.
Auf diese Weise reduziert sich durch das Vermehren der einen Größe die zweite Größe. Besonders hilfreich ist dieses Verfahren zur Ermittlung, wie viele Arbeiter, Gerätschaften oder Abläufe notwendig sind, um einen fixierten Zeitplan einzuhalten. Auf diesem Prinzip bauen die Kalkulationen verschiedener Personalbüros auf, die berechnen, ob mehr Mitarbeiter einzustellen, oder ob beim verfügbaren Auftrag zu viele Arbeiter tätig sind.
Allgemeine Vorgehensweise des antiproportionalen Dreisatzes
Im ersten Schritt zeichnet der Anwender eine kleine Tabelle mit zwei Spalten und drei Zeilen. In der Regel finden sich in der Angabe drei Werte und eine gesuchte Unbekannte.
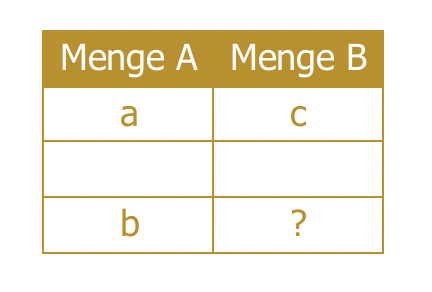
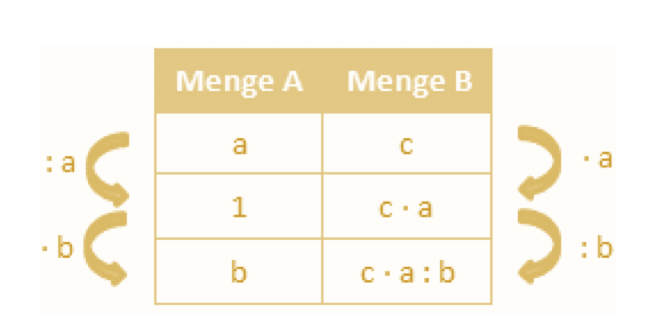
Auf diese Weise ist es möglich, komplizierte Aufgabenstellungen innerhalb kurzer Zeit zu errechnen. Oft spielt der antiproportionale Dreisatz dann eine Rolle, wenn sich zum Beispiel durch mehr Arbeiter die Arbeitszeit verkürzt. Dasselbe ereignet sich, dass mehr Geräte schneller das gewünschte Durchführen. Aus diesem Aspekt ist zu schließen, dass links oft eine Arbeitskraft und rechts die Zeit eine Rolle spielt.
Aus jeder antiproportionalen Zuordnung von x und y ergibt sich bei der Multiplikation dieser einen gleichen Proportionalitätsfaktor k: x*y =k. Stellt der Anwender den umgekehrten Dreisatz grafisch dar, ergibt sich eine Hyperbel. Als Merksatz für den antiproportionalen Dreisatz gilt, dass bei einer umgekehrten Zuordnung die Größe der einen Zahl der Kehrwert zur anderen Größe proportional ist.
Ein Beispiel – 4 Bagger und 10 Stunden
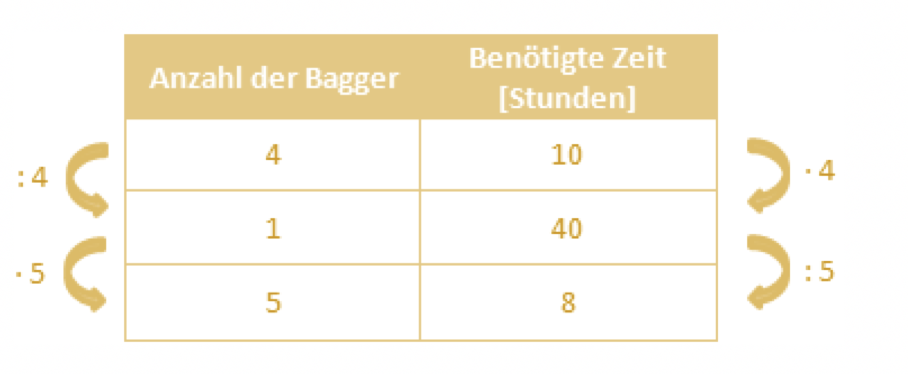
In einem praxisorientierten Beispiel tragen 4 Bagger einen großen Erdhaufen in 10 Stunden ab. Die Frage die sich nun stellt,, ist, wie lange 5 Bagger für denselben Erdhaufen benötigen?
Die Aufgabe zu lösen stellt auf den ersten Blick ein komplizierter Rechenvorgang dar. Allerdings ist es von Nutzen, den antiproportionalen Dreisatz anzuwenden. Auf der einen Seite notiert sich der Anwender die Anzahl der Bagger und auf der rechten Seite die benötigte Zeit für die Arbeit. Zu beachten ist, dass jeweils die Spalte, bei der mehr Werte zur Verfügung stehen, auf die linke Seite schreiben.

Nach der allgemeinen Vorgehensweise des antiproportionalen Dreisatzes ist es notwendig, zwischen den verfügbaren Zahlen eine 1 zu schreiben. Um diese Zahl zu erreichen, gilt es die Anzahl der Bagger durch 4 zu teilen. Im selben Schritt multipliziert der Anwender die benötigte Zeit in der ersten Zeile mal 4. Es ist zu erkennen, dass ein Bagger 40 Stunden Zeit braucht, um den Erdhaufen abzutragen.
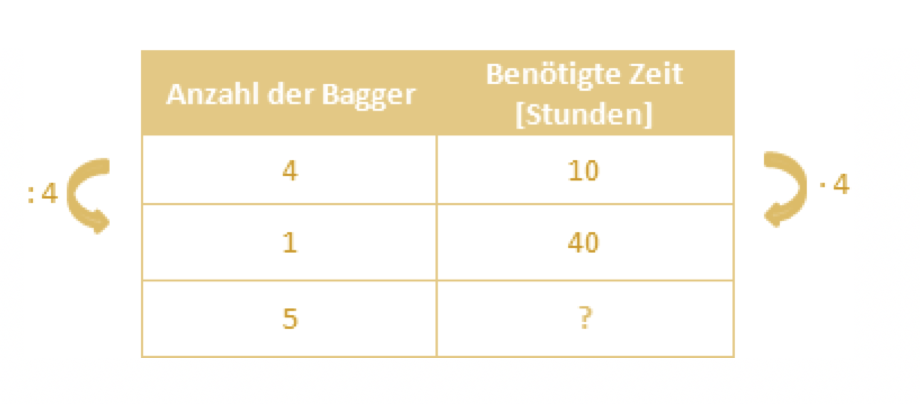
Es stellt sich allerdings die Frage, wie viel Zeit 5 Bagger für das Abtragen benötigen? Für diesen Zweck multipliziert der Mathematiker die Anzahl der Bagger an dieser Stelle mal 5 und dividiert im selben Zug die Arbeitszeit der zweiten Zeile durch 5. Daraus ergibt sich, dass 5 Bagger für das Abtragen des großen Erdhaufens 8 Stunden Arbeitszeit benötigen.
Beispiel – Maurer errichtet eine Mauer
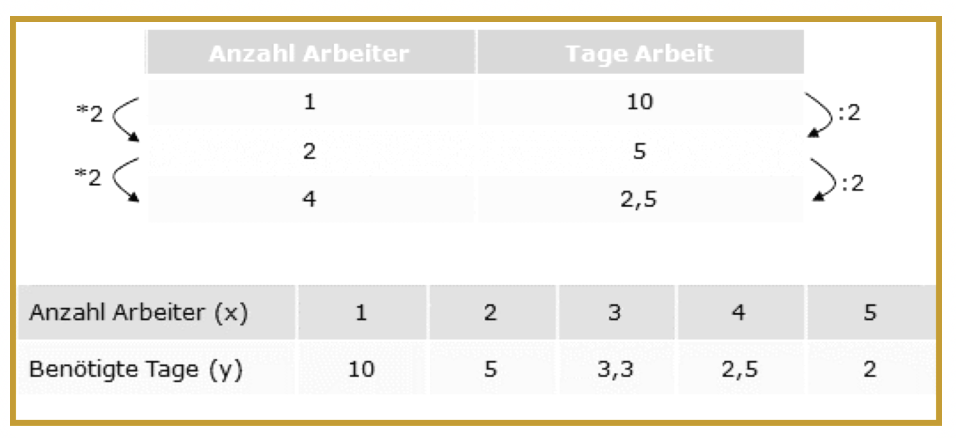
Bei einem weiteren Beispiel braucht ein Maurer 10 Arbeitstage, um die gewünschte Mauer zu errichten. Es stellt sich die Frage, wie schnell 4 Maurer dieselbe Mauer errichten.
Für diese Berechnung nutzt der Mathematiker wieder den antiproportionalen Dreisatz. Zuerst gilt es die angegebenen Werte einzutragen, 1 Maurer braucht 10 Tage und 4 Maurer brauchen x Tage. An dieser Stelle ist es möglich, im nächsten Schritt direkt auf die 4 Arbeiter zu multiplizieren und die 10 Tage durch 4 zu dividieren. Geschickt ist es allerdings, den mittleren Schritt einzubauen und zunächst mit 2 zu multiplizieren. Im gleichen Zug dividiert der Anwender die 10 Tage durch 5. Das Zwischenergebnis: 2 Arbeiter brauchen 5 Tage.
Um am Ende auf die 4 Arbeiter zu kommen, multipliziert der Mathematiker die 2 Arbeiter mal 2 und dividiert die 5 Arbeitstage durch 2. Auf diese Weise ergibt sich das Ergebnis, dass 4 Arbeiter 2,5 Tage benötigen, um eine Mauer zu errichten.
Beispiel – Fertigstellung eines Produktionsauftrags
In diesem Beispiel gilt es, zu berechnen, wie viele Produktionsmitarbeiter notwendig sind, um einen Auftrag abzuschließen. 3 Mitarbeiter benötigen für das Abschließen des Produktionsauftrages 12 Stunden. Wie lange braucht es, wenn insgesamt 8 Arbeiter am Auftrag tätig sind. Für diesen Zweck stellt der Anwender eine Tabelle auf. In der linken Spalte sind die Anzahl der Arbeiter einzutragen und in der rechten Spalte die Arbeitsstunden für den Auftrag.
In der ersten Zeile benötigen 3 Mitarbeiter 12 Stunden für den Auftrag. Um zu einem zuverlässigen Ergebnis zu kommen, dividiert der Mathematiker die 3 Mitarbeiter durch 3 und multipliziert die 12 Stunden mal 3. In der zweiten Zeile steht jetzt, dass 1 Mitarbeiter 36 Stunden für den Auftrag arbeitet.
An dieser Stelle stellt sich die Frage, wie lange 8 Mitarbeiter beschäftigt sind. Für diesen Zweck multipliziert der Anwender den einzelnen Mitarbeiter mal 8 und dividiert die 36 Stunden durch 8. Das Ergebnis lautet, dass 8 Mitarbeiter 4,5 Stunden benötigen, um den Auftrag fertigzustellen.
