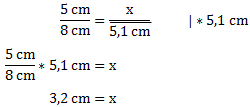Erster Strahlensatz
Der Strahlensatz kann dazu benutzt werden, unter bestimmten geometrischen Voraussetzungen unbekannte Strecken zu berechnen. Es gibt mehrere Strahlensätze von denen wir uns hier allerdings nur die ersten beiden genauer anschauen werden. Diese gelten wenn zwei sich schneidende Geraden von zwei parallelen Geraden geschnitten werden.
Erster Strahlensatz
Zunächst einmal erklären wir hier allgemein den ersten Strahlensatz. Anschließend folgen Beispiele.
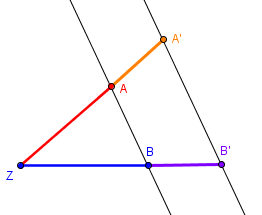
![]()
Es verhalten sich also die beiden Abschnitte auf einer Gerade genauso wie die ihnen entsprechenden Abschnitte auf der anderen Geraden.
Genauso verhält es sich, wenn sich die parallelen Geraden auf unterschiedlichen Seiten des Kreuzungspunkts Z befinden:
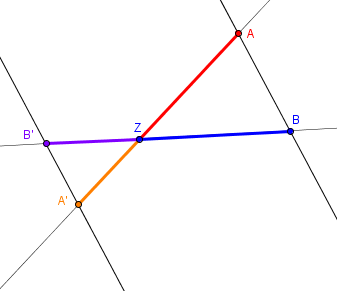
![]()
Wenn wir die Länge von 3 Seiten kennen, können wir mit dem Strahlensatz die vierte Seite berechnen. Dazu müssen wir die Formel nur zu der unbekannten Seite umformen.
Unser Lernvideo zu : Erster Strahlensatz
Beispiel 1
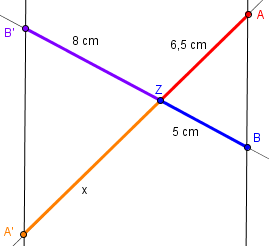
Wir möchten nun die fehlende Strecke x berechnen. Dazu benutzen wir folgende Formel:
![]()
Und setzen die bekannten Größen ein:
![]()
Und Stellen die Formel nach x um. Dazu müssen wir das x zunächst aus dem Nenner holen indem wir mit x multiplizieren.
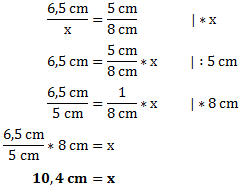
Die Strecke x ist also 10,4 cm lang.
Beispiel 2
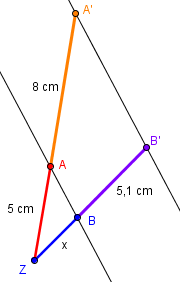
Auch hier ist die Aufgabe die fehlende Strecke x zu berechnen. Wir verwenden folgende Formel:
![]()
Natürlich hätten wir auch die andere oben genannte Formel nehmen können, dann wäre die Umformung allerdings um einiges komplizierter geworden. Deshalb nehmen wir die erste.
Wir beginnen damit die Zahlen einzusetzen und anschließend nach x umzuformen: