Erwartungswert
Was ist das Erwartungswert?
- Der Erwartungswert gibt an, welchen Wert man für eine Zufallsgröße zu erwarten hat, wenn man das Experiment, das zu ihr führt, oft ausführt. Zum Beispiel der Erwartungswert beim Würfeln eines Würfels (1+2+3+4+5+6)/6=3.5 sagt dir, dass du beim würfeln im Mittel 3.5 Augen „erwarten“ kannst.
- Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Begriff der Stochastik.
Ziel: Charakterisiere Verteilungen von Zufallsvariablen durch Kenngrößen ; Insbesondere:
a) ”durchschnittlicher Wert“ −→ Erwartungswert, z.B.
• ” mittleres“ Einkommen,
• ”durchschnittliche“ Körpergröße,
• „fairer Preis eines Spiels“
b) Streuung (Dispersion), z.B. wie stark schwankt das Einkommen, die Körpergröße etc…
Formel
- E(X) = x1 · P(X = X1 ) + x2 · P(X = x2 ) + … + Xn · P(X = Xn )
Unterschied zwischen Erwartungswert und arithmetischer Mittelwert
Das arithmetische Mittel ist ein wert der beschreibenen Statistik. Er ist definiert als Quotient der Summe aller beobachteten Werte und der Anzahl der Werte.
Z.B. Werfen wir 5 mal einen Würfel. Die beobachteten Werte seien: 1,3,3,4,6
Das arithmetische Mittel ist jetzt (1+3+3+4+6)/5 = 17/5 = 3,4
Der Erwartungswert einer Zufallsvariablen beschreibt die hingegen die Zahl, die die Zufallsvariable im Mittel annimmt.
Beim Würfel wären das 3,5.
Für unendlich viele Versuche sollte sich das arithmetische Mittel dem Erwartungswert annähern.
Kurzgefasst kann man sagen; Der Erwartungswert ist der theoretische Wert und der arithmetische Mittelwert der praktische Wert!
Unser Lernvideo zu : Erwartungswert
Beispiel 1
Wir haben eine Grafik, in der die Wahrscheinlichkeit für eine bestimmte Anzahl eingetragen wird. Ziel ist es, für diese Angaben den Erwartungswert zu berechnen.
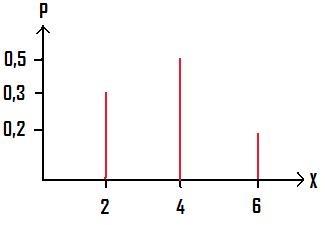
Lösung: E(X) = 2 · 0,3 + 4 · 0,5 + 6 · 0,2 = 3,8
