Euklidischer Algorithmus
Was ist der Euklidischer Algorithmus?
Der „Euklidische Algorithmus“ ist ein Verfahren zur Bestimmung des ggT zweier Zahlen, welches schon Euklid vor 2200 Jahren in seinem bekannten Mathematikwerk beschreibt.
Vorgehensweise
Wenn man zwei Zahlen a und b gegeben hat, dann bestimmt man den größten gemeinsamen Teiler ggT(a,b)von a und b folgendermaßen:
- Teile (mit Rest) die größere der beiden Zahlen durch die kleinere.
- Teile nun die kleinere der beiden Zahlen durch den Rest der bei Schritt 1 herauskommt.
- Teile nun den Rest der bei Schritt 1 herauskommt durch den Rest der bei Schritt 2 herauskommt.
- Teile nun den Rest der bei Schritt 2 herauskommt durch den Rest der bei Schritt 3 herauskommt.
- Führe dies sooft durch bis bei einer Rechnung der Rest 0 herauskommt.
- Der Divisor bei dieser Rechnung ist der ggT der Zahlen a und b.
Mit folgener Rechenschema könnt ihr eure Rechnung fortsetzen

Wir betrachten dazu jeweils einen Beispiel
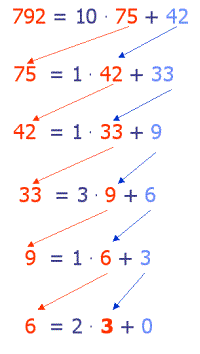
Das Beispiel zeigt, wie man mit Hilfe des Euklidschen Algorithmus‘ den ggT(792,75) bestimmt.
Im ersten Schritt fragen wir, wie häufig die zweite Zahl, also 75 ganzzahlig in der ersten, nämlich 792 enthalten ist. Diese Ganzzahldivision liefert 10 und den Rest 42. Im weiteren Verlauf werden wir sehen, dass die Zahl 10 für den weiteren Verlauf unwichtig ist, also getrost vergessen werden kann. Wesentlich ist, wir berechnen 792 mod 75 und das ist 42. Im zweiten Schritt fragen wir: Wie groß ist der Rest, wenn wir 75 ganzzahlig durch 42 teilen. Wir bestimmen also 75 mod 42. Diese Schritte wiederholen sich
Somit berechnen wir nacheinander:
792 mod 75 = 42
75 mod 42 = 33
42 mod 33 = 9
33 mod 9 = 6
9 mod 6 = 3
6 mod 3 = 0
Ist der Rest 0, ist der Algorithmus zu Ende. 3 ist der gesuchte größte gemeinsame Teiler. Da garantiert werden kann, dass der Rest irgendwann 0 ist, sagen wir, der Algorithmus terminiert.
kleiner Notiz: die hellblauen Zahlen ist immer der Rest!
Beispiel 2

das ggT ist also die Zahl 21
Die Grundidee
Die Grundidee war die Ermittlung eines größten gemeinsamen Teilers zweier Zahlen. Euklid machte sich dabei zu nutze, das sich der ggT zweier Zahlen nicht ändert, wenn man die kleinere von der größeren Zahl subtrahiert. Also wurde jeweils immer die Kleinere von der größeren Zahl subtrahiert. Solange bis irgendwann die kleinere Zahl 0 ist. Die größere ist dann der größte gemeinsame Teiler.
Das subtrahieren wurde in der modernen Mathematik durch das Teilen mit Restbildung ersetzt. Auch kann man den Algorithmus nicht nur für natürliche Zahlen anwenden sondern inzwischen auch allgemein für Polynome.
