Extremwerte
Extremwerte, auch als Extrema (Einzahl: Extremum) bekannt, sind alle Hoch- und Tiefpunkte einer Funktion. Hochpunkte werden auch Maximum, Tiefpunkte auch Minimum genannt. Dabei wird der jeweilgen x-Wert als Extremwert bezeichnet und bildet in Kombination mit dem dazugehörigen y-Wert die Extremstelle.
Die unten dargestellte Beispielfunktion besitzt zwei Hochpunkte (rote Pfeile) und einen Tiefpunkt (grüner Pfeil). Hierbei ist der Hochpunkt mit dem gefüllten roten Pfeil ein globaler Hochpunkt, während der andere rote Pfeil lediglich auf einen lokalen Hochpunkt weist. Der einzige lokale Tiefpunkt ist automatisch auch der globale Tiefpunkt.
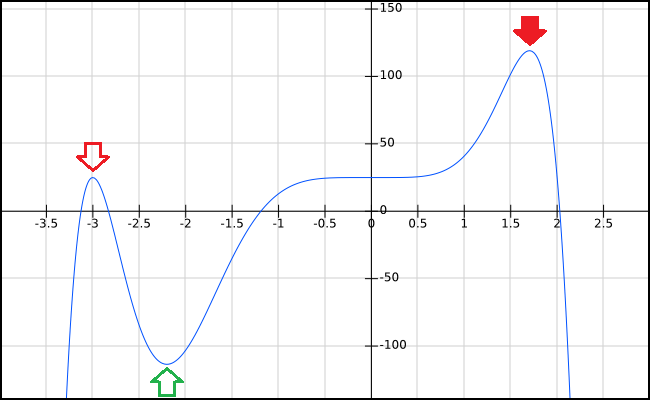
Wo genau sich die Extremwerte befinden, lässt sich auf der 1. Ableitung (hier rot), die im folgenden Graph dargestellt ist. Schneidet die 1. Ableitung die x-Achse, ist also f ‚(x) = 0, liegt in der Stammfunktion (hier blau) ein Extremwert vor. Dies ist in der gezeigten Funktion bei x1 = -3,1 und x2 = -2,8 sowie x1 = +2,0 der Fall.
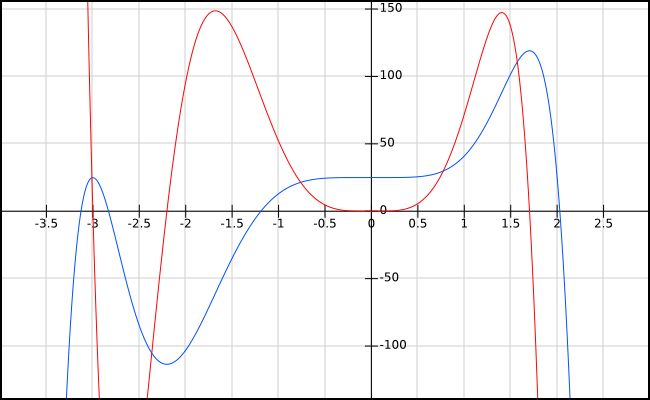
Voraussetzungen für die Existenz eines Extremwertes sind somit zwei Bedingungen:
- Notwendige Bedingung: f ‚(x) = 0
- Hinreichende Bedingung: f “(x) ≠ 0
→ wenn f´´(x) > 0, dann Tiefpunkt
→ wenn f´´(x) < 0, dann Hochpunkt
Beispiel 1
f(x) = x3 + 6x2 – 9x
1. Schritt
Zunächst ist die 1. Ableitung zu bilden.
f ´(x) = 3x2 + 12x – 9
2. Schritt
Die 1. Ableitung wird dann gleich Null gesetzt.
f ´(x) = 0
3x2 + 12x – 9 = 0
3. Schritt
Als nächstes die quadratische Gleichung in die Normalform bringen.
3x2 + 12x – 9 = 0 |:3
x2 + 4x – 3 = 0
4. Schritt
Nun kann die p–q-Formel angewendet werden.
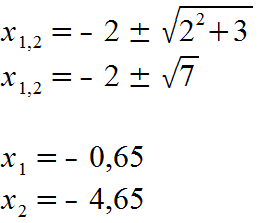
Das sind die x-Koordinaten unserer Extremwerte.
5. Schritt
Um die y-Werte zu ermitteln, müssen x1 und x2 in f(x) eingesetzt werden.
f(x1) = (-0,65)3 + 6 ⋅ (-0,65)2 – 9 ⋅ (-0,65) = 8,11
f(x2) = (-4,65)3 + 6 ⋅ (-4,65)2 – 9 ⋅ (-4,65) = 71,04
6. Schritt
Um zu prüfen, ob es sich um einen Hoch- oder Tiefpunkt handelt, wird die hinreichende Bedingung verwendet.
Zunächst ist die 2. Ableitung zu bilden.
f ´´(x) = 6x + 12
Dann x1 und x2 in f(x) eingesetzen.
| f ´´(-0,65) = 6 ⋅ (-0,65) + 12 = 8,1 > 0 | → Tiefpunkt |
| f ´´(-4,65) = 6 ⋅ (-4,65) + 12 = -15,9 < 0 | → Hochpunkt |
Im Ergebnis erhalten wir einen Tiefpunkt bei (-0,65 | 8,11) und einen Hochpunkt bei (-4,65 | 71,04).
Beispiel 2
f(x) = 0,25x2 + 2x – 12
1. Schritt
1. Ableitung bilden
f ‚(x) = 0,5x + 2
2. Schritt
1. Ableitung gleich Null setzen
| f ´(x) = 0 | |
| 0,5x + 2 = 0 | |-2 |
| 0,5x = -2 | |:0,5 |
| x = -4 |
3. Schritt
Ermitteln der y-Koordinate
f(-4) = 0,25 ⋅ (-4)2 + 2 ⋅ (-4) – 12
f(-4) = -16
4. Schritt
Prüfen, ob Hoch- oder Tiefpunkt:
f ´´(x) = 0,5
f ´´(-4) = 0,5 > 0 → Tiefpunkt
Das Ergebnis ist ein Tiefpunkt bei (-4 | -16).
