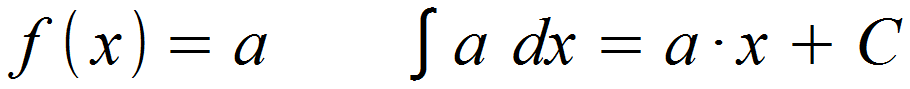Faktorregel bei Integration
Befindet sich ein Faktor vor der Potenz, der unabhängig von der Variablen x ist, kann dieser aus dem Integral gezogen werden und nach dem Aufleiten einfach mit dem Ergebnis des Integrals multipliziert werden.
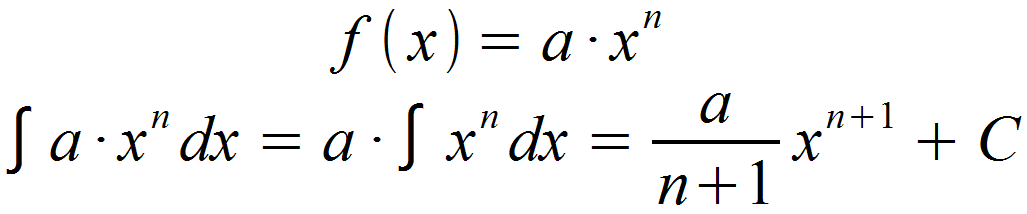
Es wird also zunächst der Faktor a aus dem Integral gezogen und die übrige Potzenz regulär nach der Potenzregel aufgeleitet. Anschließend kann der Faktor a wieder mit dem Bruch multipliziert werden. In der Formel wurde der Faktor direkt in den Zähler des Bruchs gezogen.
Man muss bei der Definition von a aufpassen, dass dieser wirklich unabhängig von x ist. Das bedeutet, dass kein x in irgendeiner Art und Weise herausgezogen wird, bevor das Integral nicht gelöst wurde.
Unser Lernvideo zu : Faktorregel bei Integration
Beispiel 1
Folgende Potenzfunktion soll aufgeleitet werden.
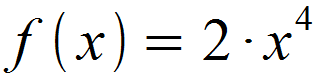
Zunächst identifizieren wir den Faktor a vor der Potenz und den Exponenten n.
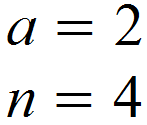
Eingesetzt in die Formel ergibt sich somit folgendes Integral:
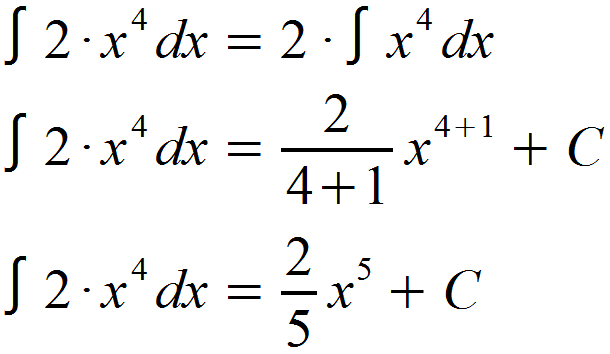
Wir ziehen also den Faktor 2 aus dem Integral und leiten regulär nach der Potenzregel auf. Anschließend multiplizieren wir das Resultat des Integrals wieder mit dem Faktor 2.
Beispiel 2
Die folgende konstante Funktion soll aufgeleitet werden.
![]()
- Im Folgenden wird gezeigt, wie eine Konstante Schritt für Schritt mit der Faktor- und Potenzregel aufgeleitet wird. Es ist sicherlich von Vorteil, dies verstanden und beim Aufleiten im Hinterkopf zu haben. Für die Anwendung reicht im Grunde auch die verkürzte Fassung, die du weiter unten als Hinweis findest.
Wir können die Funktion als Polynomfunktion 0. Grades betrachten, da jede Potenz mit 0 als Exponent gleich 1 ist.
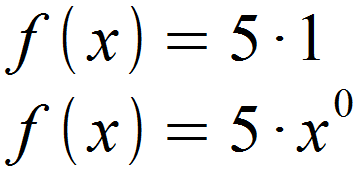
Jetzt können wir wieder den Faktor a vor der Potenz und den Exponenten n identifizieren.
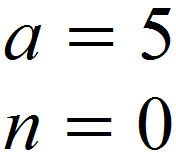
Diese können wieder regulär in die Formel eingesetzt werden.
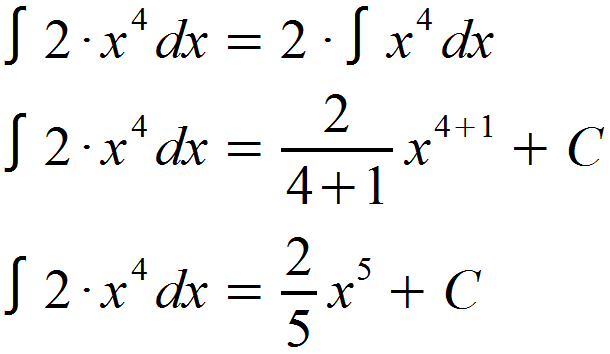
Wir ziehen also erneut den Faktor 5 heraus und multiplizieren diesen wieder mit dem Rest des Integrals, nachdem der Rest ganz normal mit der Potenzregel aufgeleitet wurde.
Also ist die Aufleitung kurz gefasst:
![]()

Die komplette Herleitung muss nicht jedes Mal runtergeschrieben werden, wenn eine Konstante aufgeleitet wird. Alternativ kann einfach folgende Integrationsregel behalten werden: