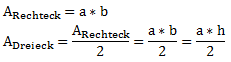Flächeninhalt eines Dreiecks
Den Flächeninhalt eines Dreiecks können wir mithilfe einer Seite und der dazugehörigen Höhe berechnen. Die Formel dafür lautet:
![]()
Das a bezieht sich dabei auf eine Seite des Dreiecks und das h auf die dazugehörige Höhe.
Der Flächeninhalt wird allgemein mit dem Buchstaben A bezeichnet. Seine Einheit richtet sich nach der Einheit der gegebenen Strecke und Höhe. Diese müssen vor der Berechnung auf dieselbe Einheit umgerechnet werden. Sind a und h in Zentimeter gegeben ist die Einheit von A cm². Sind a und h in Meter gegeben ist die Einheit von A m².
Lerntool zu Flächeninhalt eines Dreiecks
Unser Lernvideo zu : Flächeninhalt eines Dreiecks
Die Angaben zum Flächeninhalt von Dreiecken
Für eine verbesserte Übersicht liefern wir nochmals die wichtigsten Grundbegriffe im Zusammenhang mit einem Dreieck.
- Grundseite: g
- Höhe: h
- Die Seiten des Dreiecks: a, c, b
- Die Punkte des Dreiecks: A, B, C
Grundsätzlich macht es Sinn, den Flächeninhalt der Dreiecke erst einmal herzuleiten, um die Größen zu verstehen. Eigentlich müssen wir nichts weiter tun, als die Länge mit der Breite des Dreiecks zu multiplizieren. Jedes Dreieck besitzt eine Grundseite und eine Höhe, die wiederum die Grundseite in zwei Teile spaltet.
Die Höhe in einem Dreieck markiert zwei rechtwinklige Dreiecke im Inneren. Jetzt spiegeln wir zwei neue, rechtwinklige Dreiecke kongruent und es entsteht ein Rechteck.
Grundsätzlich ist davon auszugehen, dass der Flächeninhalt eines Rechtecks doppelt so groß ist wie das der Dreiecke. Zunächst einmal kann man den Flächeninhalt der Rechtecke herleiten und diese im Anschluss addieren. Teilen wir das Ergebnis durch 2 – haben wir den Flächeninhalt der Rechtecke. Daraus ergibt sich unsere Formel für die Berechnung.
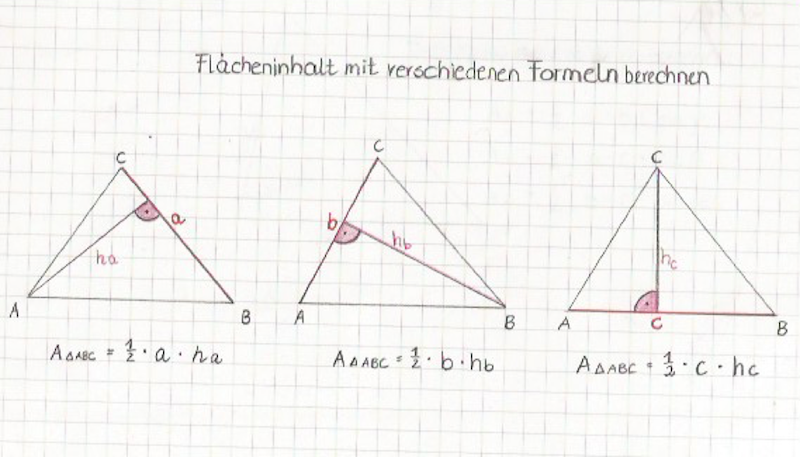
Drei Rechenwege, den Flächeninhalt von Dreiecken zu berechnen
Wir unterscheiden drei verschiedene Rechenformeln und Rechenwege, wie wir zum Flächeninhalt des Dreiecks kommen:
- Wie oben genannt haben wir bereits ausgehend von der Höhe und der Grundlinie für rechtwinklige Dreiecke und für gleichseitige Dreiecke eine passende Rechenformel gefunden: A = ½ • g • h
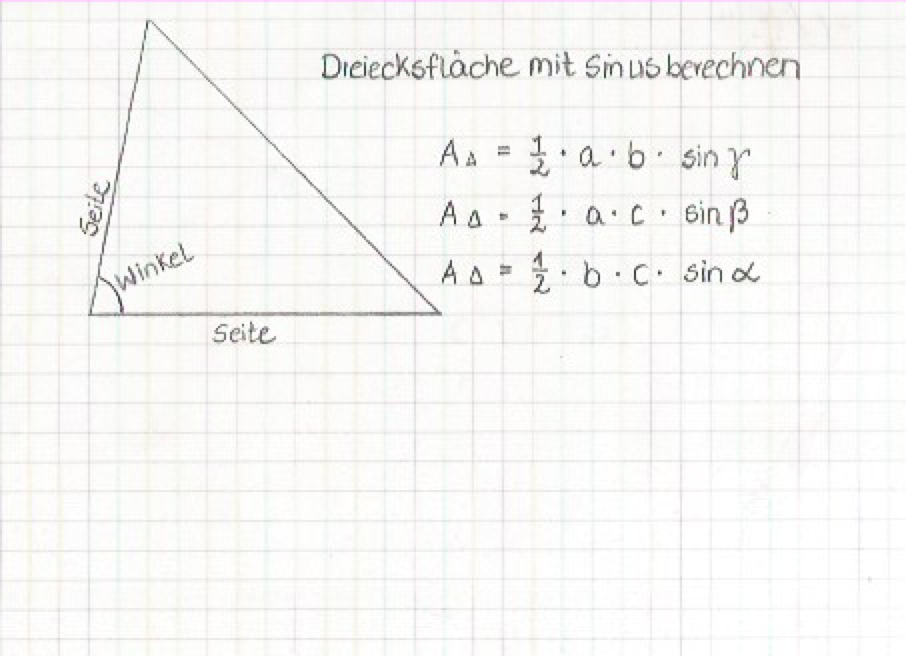
- Zudem könnt ihr mit einer Determinante im Koordinatensystem die Fläche von Dreiecken berechnen: A = ½ • | AB AC I
- Ausgehend von zwei Seiten des Dreiecks und dem Sinus des Winkels ergibt sich eine zweite Formel: A = ½ • a • b • sin
Beispiel
Von einem Rechtwinkligen Dreieck haben wir alle drei Seiten gegeben:
a = 4 cm
b = 3 cm
c = 5 cm
Wie groß ist der Flächeninhalt?
Wir brauchen für die Berechnung eine Seite und die dazugehörige Höhe. Wir zeichnen das Dreieck zunächst:
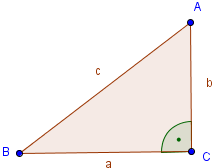
Wir wählen die Seite a als Grundseite. Die dazugehörige Höhe ist die Seite b (da es sich um ein rechtwinkliges Dreieck handelt). Anschließend müssen wir die Werte nur noch in die Formel einsetzen:
![]()
Wir hätten natürlich auch die Seite b als Grundseite wählen können, dann wäre die Seite a die dazugehörige Höhe gewesen. Das Ergebnis wäre dasselbe gewesen. Nur wenn wir die Seite c als Grundseite gewählt hätten, wäre es schwieriger geworden, da wir die Höhe hier nicht direkt wissen. Diese müssten wir zeichnerisch bestimmen. Auch dann wäre das Ergebnis natürlich identisch, aber der Weg dorthin wäre schwieriger.
Herleitung der Formel für den Flächeninhalt
Für den Flächeninhalt eines Rechtecks kennen wir folgende Formel:
![]()
Wir zeichnen nun um unser Dreieck ein Rechteck, so dass die Höhe h gleich der Seite b (vom Rechteck) ist und die Seite a erhalten bleibt:
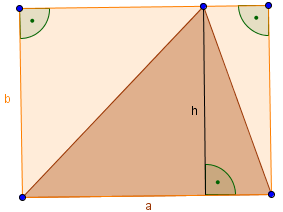
Wir teilen nun dieses Rechteck an der Höhe h in zwei Teile:
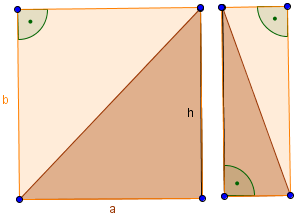
Wir sehen deutlich, dass auf der linken und auch auf der rechten Seite die Diagonale die beiden Teile jeweils in zwei genau gleichgroße Teile teilt. Daraus geht hervor, dass der Flächeninhalt des dunkel gezeichneten Dreiecks genau halb so groß ist, wie der des helleren Rechtecks. Für die Flächenberechnung eines Dreiecks können wir die Fläche eines Rechtecks also einfach halbieren. So kommen wir auf die Formel: