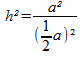Flächeninhalt eines regelmäßigen Sechsecks
Nun zeigen wir euch, wie ihr den Flächeninhalt eines regelmäßigen Sechsecks berechnen könnt.
Dazu müssen wir zunächst wissen, wie sich ein solches definiert:
Definition: Ein regelmäßiges Sechseck, oder Hexagon, hat sechs gleichlange Seiten und sechs gleichgroße Winkel.
In der Abbildung sehen wir ein regelmäßiges Sechseck. Alle Seiten sind gleich lang und alle Winkel gleich groß.
Lerntool zu Flächeninhalt eines regelmäßigen Sechsecks
Unser Lernvideo zu : Flächeninhalt eines regelmäßigen Sechsecks
Berechnung des Flächeninhalts
Zur Berechnung des Flächeninhalts teilen wir das Sechseck in sechs gleich große Dreiecke.
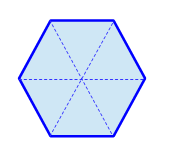
Nun haben wir sechs gleich große Dreiecke. Diese Dreiecke sind Gleichseitige Dreiecke, was bedeutet, dass die Seiten alle gleich lang sind.
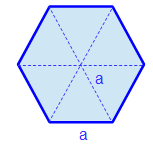
Um nun den Flächeninhalt berechnen zu können, können wir ein Dreieck berechnen und das Ergebnis mal sechs rechnen. So ergibt sich der Flächeninhalt des Rechtecks. Um später eine allgemeine Rechnung zu haben, nutzen wir die allgemeinen Angaben.
Schritt 1: Die Berechnung eines Dreiecks.
Die Rechenforschrift lautet: A= 1/2 g • h. Hier ist g = a und uns fehlt noch die Höhe h. Diese können wir mit dem Satz des Pythagoras errechnen, a² + b² = c².
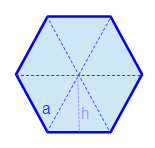
In unserem Fall ist die Hypothenuse = a und eine Kathete a/2. Die andere Kathete h wird gesucht. Daher lautet die Rechenformel: