Gemischte Zahlen
Aufbau der gemischten Zahlen einfach erklärt
Gemischte Zahlen bestehen aus einer ganzen Zahl gefolgt von einem Bruch:
Um diese Zahlen in Dezimalzahlen oder einen einfachen Bruch umzuwandeln, müssen wir zunächst einmal verstehen, wie diese Zahlen aufgebaut sind. Sie haben den Vorteil, dass man deutlich schneller die Größenordnung einschätzen kann als bei Brüchen. Wir wissen bei dem ersten Beispiel sofort, dass die Zahl zwischen 1 und 2 liegt. Bei dem zweiten zwischen 9 und 10 und bei dem dritten zwischen 7 und 8. Die Zahl liegt also immer zwischen der führenden ganzen Zahl und der nächst höheren. Der Bruch bildet quasi die Nachkommastellen. Im ersten Beispiel ist 
. Die Zahl könnte also in dezimaler Schreibweise auch als 1,5 geschrieben werden.
Der Vorteil wird deutlich bei dem Beispiel 
. Hier ist die dezimale Schreibweise 7,28571428571… beziehungsweise 
. Im Gegensatz dazu ist 
doch deutlich schöner und kürzer zu schreiben. Man sieht sehr schnell wie groß die Zahl ist und muss relativ wenig schreiben.
Begriffe und Definitionen auf einen Blick
- Ist bei einem Bruch der Zähler kleiner als der Nenner – haben wir es mit einem echten Bruch zu tun.
- Ist aber der Zähler größer als der Nenner, sprechen wir von einem unechten Bruch.
- natürliche Zahl: Hier ist von einem Sonderfall die Rede, indem der Zähler ein Vielfaches vom Nenner ist. Haben wir im Zähler zum Beispiel eine 36 und im Nenner eine 6, können wir beide Zahlen kürzen und erhalten im Ergebnis die 6.
- gemischte Zahlen: Haben wir eine Summe aus natürlichen Zahlen und einem echten Bruch, handelt es sich um natürliche Zahlen.
Gemischte Zahlen besser verstehen
Gehen wir auf unser ursprüngliches Tortenmodell zurück – so können wir bei
von einer ganzen Torte und einer halben ausgehen. Nun müssen wir mit diesen Zahlen und den unterschiedlichen Arten umgehen und rechnen können. Von daher ist es praktisch, diese gemischten Zahlen in Brüche umzurechnen.
Der Nenner bleibt wie in diesem Beispiel gleich bei 2. Dann multipliziert du einfach diese vordere Zahl, sprich 1, mit dem Nenner – 2. Anschließend können wir die beiden Brüche addieren, schließlich haben sie einen gemeinsamen Nenner:
.
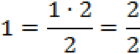Diesen Rechenweg haben wir weiter unten nochmals detailliert dargestellt. Wir raten euch dazu, die Umrechnung mit ein paar gemischten Zahlen und Übungsaufgaben zu trainieren, um hier eine gewisse Routine im Umgang mit diesen Zahlen zu bekommen.
ABER ! Der Nenner darf niemals den Wert 0 annehmen.
Unser Lernvideo zu : Gemischte Zahlen
Umrechnung: Gemischte Zahl in Bruch
Um eine gemischte Zahl in einen Bruch umzurechnen, müssen wir die ganze Zahl die vorne steht zunächst in einen Bruch umrechnen der den gleichen Nenner hat wie der folgende Bruch. Anschließend können wir beide Brüche einfach addieren.
1. Beispiel: Gemischte Zahlen umrechnen
Um diese gemischte Zahl in einen Bruch umzurechnen, müssen wir die 1 in einen Bruch mit dem Nenner 2 umrechnen. Wir erweitern dafür die 1 mit der 2 um den Zähler des neuen Bruchs zu erhalten:
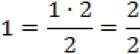
Im nächsten Schritt addieren wir den Bruch der gemischten Zahl. Da die Nenner bereits gleich sind, brauchen wir nur die Zähler zu addieren:
Man kann also schreiben:
2. Beispiel: Gemischte Zahlen umrechnen
Als erstes müssen wir wieder die 5 in einen Bruch umrechnen:
Jetzt können wir die beiden Brüche addieren:
Und erhalten das Ergebnis.
Umrechnung: Gemischte Zahl in Dezimalzahl
Wir können hier natürlich genau wie eben vorgehen und den Bruch zunächst einmal in einen einfachen Bruch umrechnen und diesen dann in eine Dezimalzahl umwandeln. Wir können uns aber ein wenig Zeit sparen, indem wir die gemischte Zahl direkt in eine Dezimalzahl umwandeln.
Die Zahl vor dem Komma haben wir ja schon. Sie ist identisch mit der ganzen Zahl am Anfang der gemischten Zahl. Uns fehlen also nur die Nachkommastellen. Diese können wir ermitteln, indem wir den Bruch in eine Dezimalzahl umwandeln. Dazu müssen wir einfach die Division die der Bruch beschreibt durchführen.
Beispiel: Gemischte Zahlen umrechnen
Die 7 steht als Zahl vor dem Komma fest. Wenn wir 3 durch 4 teilen, bekommen wir als Ergebnis 0,75. Das Ergebnis ist also:
