Das Koordinatensystem
Ein Koordinatensystem hilft uns Punkte an einer bestimmten Position zeichnen zu können. Ein Koordinatensystem ist erst einmal ein Raum, in dem jede Position eine bestimmte Koordinate hat.
Eine Koordinate besteht dabei immer aus einem x-Wert und einem y-Wert. Wenn man also einen x- und y-Wert gegeben hat, ist damit eine ganz bestimmte Position im Koordinatensystem gemeint.
Rechner Das Koordinatensystem
Unser Lernvideo zu : Das Koordinatensystem
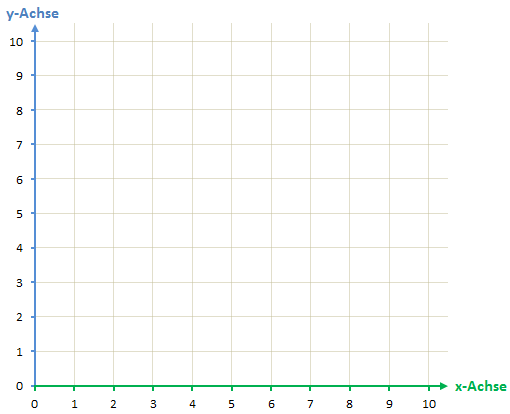
Diese Abbildung zeigt ein typisches Koordinatensystem. Ein Koordinatensystem zeichnet man am besten immer auf Karopapier.
Die x-Achse ist die waagerechte Achse. Sie befindet sich am unteren Rand des Koordinatensystems. Man kann sich diese Achse wie einen Zahlenstrahl vorstellen. Auch die Zahlen schreiben wir wie beim Zahlenstrahl in regelmäßigen Abständen (zum Beispiel jedes Kästchen eine Zahl). Wir beginnen dabei ganz links mit der 0 und erhöhen die Zahl dann immer um 1. Später kann man auch um andere Zahlen erhöhen (beispielsweise um 0,5 oder 2). Wichtig ist, dass man pro Kästchen immer um den gleichen Wert erhöht.
Die y-Achse ist die senkrechte Achse. Sie befindet sich am linken Rand des Koordinatensystems. Auch die y-Achse ist wie ein Zahlenstrahl. Unten befindet sich die 0 und nach oben steigen die Zahlen an. Wichtig ist, dass sich die x- und y-Achse genau bei den beiden Nullpunkten schneiden.
Ans Ende jeder Achse machen wir einen Pfeil, der anzeigt, dass die Zahlenwerte in diese Richtung ansteigen. Außerdem schreiben wir neben die x-Achse ein „x“ (oder „x-Achse) und neben die y-Achse ein „y“ (oder „y-Achse“).
Damit ist das Koordinatensystem fertig.
Punkt in das Koordinatensystem eintragen
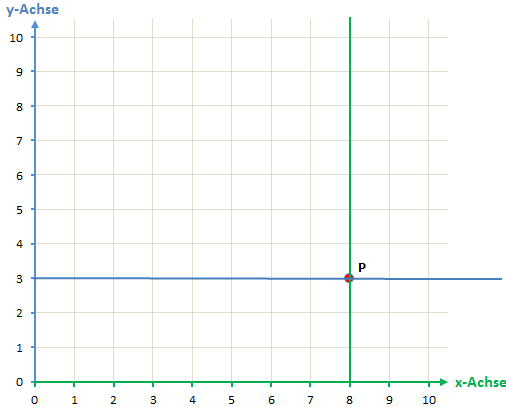
Folgenden Punkt wollen wir nun in das Koordinatensystem eintragen:
P(8/3)
Der Punkt (P) ist in x- und y-Koordinaten gegeben. Als Erstes steht immer die x-Koordinate gefolgt von einem Trennzeichen (hier „/“ oder auch „;“). Die zweite Zahl ist dann die y-Koordinate.
Allgemein: P(x/y)
Wir haben also einen x-Wert von 8 und einen y-Wert von 3. Um diesen Wert nun einzutragen, müssen wir auf der x-Achse den Wert 8 suchen. Von diesem Wert zeichnen wir uns im Kopf eine senkrechte Linie nach oben (grüne Linie). Anschließend suchen wir die 3 auf der y-Achse und zeichnen (im Kopf) eine waagerechte Linie nach rechts (blaue Linie). Dort wo sich diese beiden Linien schneiden, ist der Punkt P.
Dreieck in das Koordinatensystem eintragen
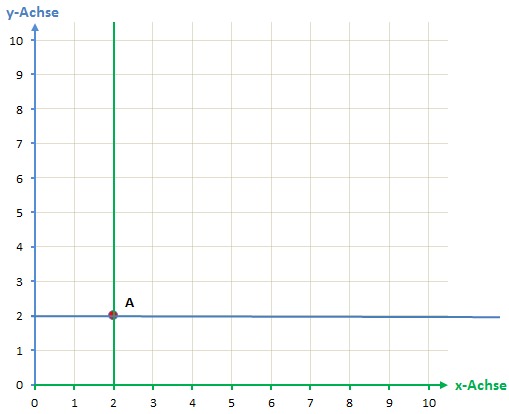
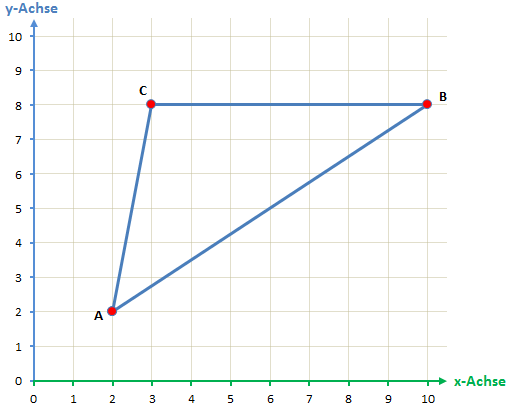
Das Dreieck mit den Punkten A(2/2), B(10/8) und C(3/8) soll in das Koordinatensystem eingetragen werden.
Wir beginnen mit den ersten Punkt A(2/2). Wir denken uns also eine senkrechte Linie bei x = 2 und eine waagerechte Linie bei y = 2. Dort wo sich die beiden Linien schneiden befindet sich der Punkt A.
Genauso gehen wir auch mit den Punkten B und C vor:
B(10/8): x-Koordinate 10, y-Koordinate 8
C(3/8): x-Koordinate 3, y-Koordinate 8
Anschließend müssen die Punkte nur noch verbunden werden:
Koordinatensystem mit negativen Koordinaten
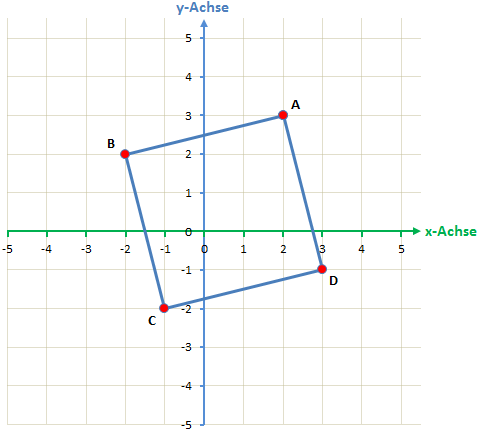
Es soll folgendes Quadrat gezeichnet werden:
A(2/3)
B(-2/2)
C(-1/-2)
D(3/-1)
Wir sehen, dass es hier auch negative Koordinaten gibt. Wir müssen also das Koordinatensystem so zeichnen, dass beide Achsen auch die negativen Zahlen abdecken. Wichtig ist dabei, dass der Schnittpunkt von x- und y-Achse immer im Nullpunkt beider Achsen liegt. Das Einzeichnen der Punkte funktioniert aber ansonsten genauso. Das Quadrat sieht dann folgendermaßen aus.
Koordinaten mit Komma
Es kann natürlich auch passieren, dass ein Punkt keine ganzzahligen Koordinaten enthält. Im Prinzip ist dies kein Problem. Wir können die Koordinaten auf dieselbe Weise eintragen.
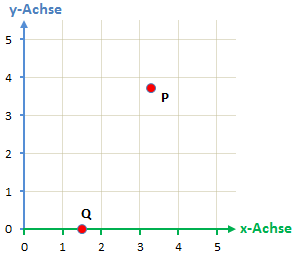
Beispiel P(3,3/3,7), Q(1,5/0)
Für den Punkt P denken wir uns wieder ein senkrechte Linie bei x = 3,3 und eine waagerechte Linie bei 3,7. Dabei ist es wegen der Kommazahlen schwierig die Position exakt zu bestimmen. Wir müssen also ein bisschen schätzen. Wir wissen, dass 3,3 dichter an der 3 ist als an der 4. Wir zeichnen 3,3 also zwischen 3 und 4 und ein bisschen dichter zu der 3 hin. Bei der 3,7 gehen wissen wir das diese ebenfalls zwischen der 3 und der 4 liegt. Außerdem liegt sie dichter an der 4 als an der 3. Wir Zeichnen sie also dementsprechend ein bisschen dichter zu der 4 hin.
Leichter ist es bei dem Punkt Q. Die x-Koordinate 1,5 liegt exakt in der Mitte zwischen 1 und 2. Die y-Koordinate 0 liegt bei y = 0, also genau auf der Linie der x-Achse.
 +-
+-
Interessante Fragen und Antworten zu Das Koordinatensystem
Wie kann man bei einem Koordinatensystem ablesen, um wie viel eine Parabel gestreckt/gestaucht ist? |
| Bei einer Standardgleichung f(x)=ax²+bx+c kann in einem Koordinatensystem abgelesen werden, ob die Parabel gestreckt oder gestaucht ist, müssen die folgenden Anweisungen beachtet werden. So kann der Scheitelpunkt an dem Punkt abgelesen werden, welcher sich rechts bzw. links vom Scheitelpunkt befindet. Diesen Punkt findest du entlang der x-Achse. Wenn du diesen Punkt gefunden hast, schaust du nach wo sich der y-Wert des Graphen befindet. Bei der Normalparabel ist dieser Wert 1. Somit ist a= 1. Ist der Wert kleiner als eins, ist die Parabel gestaucht. Bei einem Wert größer als null, wir von einer gestreckten Parabel gesprochen. Diese Vorgehensweise funktioniert jedoch nur bei leichten Gleichungen. Bei allen anderen Gleichungen, muss ein Gleichungssystem verwendet werden. |
Wie viele Achsen hat ein kartesisches Koordinatensystem? |
| Ein kartesisches Koordinatensystem hat zwei Achsen. Die horizontale (waagerechte )Achse in diesem kartesischen Koordinatensystem ist die x-Achse. Diese Achse verläuft von links nach rechts. In vielen Büchern wird die x-Achse mit dem Begriff Abszisse gleichgesetzt. Dahin gegen wird die horizontale (senkrechte) Achse im kartesischen Koordinatensystem y-Achse genannt. Diese verläuft von oben nach unten. Als Synonym für die y-Achse, finden man in der Fachliteratur den Begriff Ordinatenachse. Die y-Achse und die x-Achse verhalten sich senkrecht zu einander. Aus diesem Grund ist das kartesisches Koordinatensystem ein orthogonales Koordinatensystem. Da die beiden Koordinatenachsen sich schneiden, gibt es vier voneinander getrennte Abschnitte in jeder Ebene. Diese Abschnitte werden auch als Quadranten bezeichnet.. |
Wie viele Quadranten hat ein Koordinatensystem? |
| Ein zweidimensionales Koordinatensystem hat vier Quadranten. Die Achsen begrenzen diese jeweils in zwei Richtungen. In die beiden anderen Richtungen sind die Quadranten unendlich lang, sodass ein Quadrant grundsätzlich einen unendlichen Flächeninhalt hat, welcher innerhalb einer Aufgabenstellung jedoch begrenzt werden kann.Bei einem Koordinatensystem mit klassischer Beschriftung (waagerechte x-Achse, senkrechte y-Achse) liegt der erste Quadrant oben rechts, wird also links von der y-Achse und unten von der x-Achse begrenzt. Die folgenden drei Quadranten werden dann gegen den Uhrzeigersinn benannt. Der zweite Quadrant liegt also links neben dem ersten, der dritte unterhalb des zweiten und der vierte rechts neben dem dritten beziehungsweise unterhalb des ersten.
Punkte, die auf einer der beiden Achsen liegen sowie der Nullpunkt werden keinem Quadranten zugeordnet, da auch die Achsen selbst nicht zu einem Quadranten gehören, sondern diese lediglich begrenzen. Quadranten berühren demnach die beiden Achsen nur, schließen sie aber nicht ein. |
