Mittelsenkrechte konstruieren
Die Mittelsenkrechte ist eine Gerade, die senkrecht zu einer Strecke verläuft und diese Strecke in der Hälfte teilt. Formal ist die Definition, dass die Mittelsenkrechte (oder auch Streckensymmetrale) die Menge aller Punkte ist, die von zwei gegebenen Punkten den gleichen Abstand haben. Dabei haben wir zwei gegebene Punkte und jeder Punkt von der Mittelsenkrechten hat den gleichen Abstand zu dem einen Punkt, aber gleichzeitig auch zu dem anderen. In der Mathematik benötigt man in den verschiedensten Situationen eine Mittelsenkrechte, um z.B. die Höhe eines gleichschenkligen Dreiecks ermitteln zu können.
Die Mittelsenkrechte teilt eine Strecke in der Mitte und schneidet sie im rechten Winkel, also 90°. Wir zeigen euch nun wie man eine solche Mittelsenkrechte mit Zirkel konstruiert.
Zuerst haben wir eine gegebene Strecke. Wichtig ist, dass es sich um eine Strecke und nicht um eine Gerade oder Halbgerade handelt.

In der Abbildung haben wir eine Strecke, die mit zwei Punkten abgeschlossen ist. An diesen beiden Endpunkten setzen wir den Zirkel an. Der Radius den wir zeichnen ist an beiden Punkten der selbe und muss größer als die Hälfte der Strecke sein. Also lieber größer als kleiner.
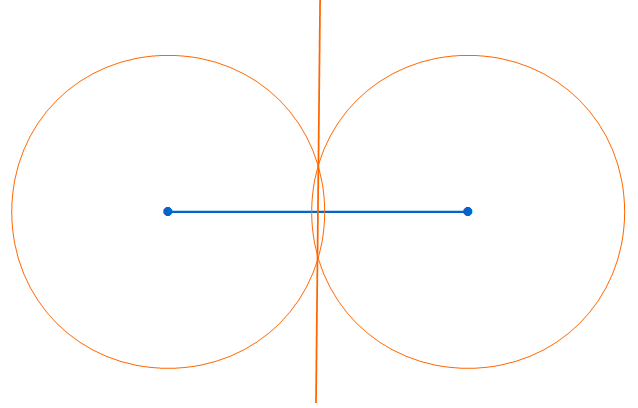
Es wurden zwei orange Kreise um die Endpunkte der Strecke gezeichnet. Beide haben den selben Radius und sind länger als die Hälfte der Strecke. Die beiden Kreise schneiden sich in zwei Punkten.
Unser Lernvideo zu : Mittelsenkrechte konstruieren
Als nächsten zeichnen wir eine Gerade durch die Schnittpunkte der beiden Kreise.
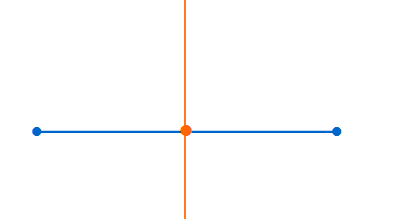
Genau durch die Schnittpunkte der Kreise ist eine Gerade gezeichnet.
Die Gerade schneidet die Strecke genau in der Mitte und mit einem rechten Winkel.
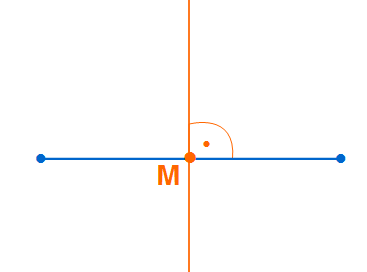
Somit haben wir recht schnell eine Mittelsenkrechte konstruiert ohne die Strecke messen zu müssen. Wenn man die Schritte beachtet, hat man immer genau die Mitte und eine Strecke die durch eine Gerade im rechten Winkel geschnitten wird.
Übt ein bisschen diese Konstruktion, denn je öfter man dieses macht, desto tiefer sitzt die Abfolge und man vergisst es nicht mehr.
