Gleichungen umformen
Gleichungen werden uns in Mathematik noch viele begegnen. Deshalb ist es wichtig, dass man Gleichungen sicher umformen und lösen kann.
Unser Lernvideo zu : Gleichungen umformen
Beispiel 1: Gleichungen umformen
Wir kennen das Umformen von Gleichungen schon aus der Grundschule. Den meisten ist nur nicht bewusst, dass sie auch dort schon Gleichungen umgeformt haben. Hier ein Beispiel:
![]()
Diese oder ähnliche Rechnungen löst man in der Grundschule. Man kann dies auch so schreiben:
![]()
Das x ist dabei eine variable die theoretisch jede beliebige Zahl annehmen kann. In diesem Beispiel gibt es aber natürlich nur eine passende Zahl. Wir können die Gleichung nun umformen. Dieses nennt man Äquivalenzumformung. Das Wort bedeutet, dass wir auf beiden Seiten der Gleichung die Gleiche Umformung vornehmen.
Wir wollen das x berechnen. Deshalb ist das Ziel, dass dieses alleine auf einer Seite steht. Die Gleichung soll also mit „x =“ anfangen oder mit „= x“ aufhören. Dazu müssen wir die 4 auf die andere Seite des Gleichzeichens bringen. Dies machen wir, indem wir auf beiden Seiten -4 rechnen. Als Symbol das wir auf beiden Seiten -4 rechnen, schreiben wir -4 hinter einen senkrechten Strich hinter die Ausgangsgleichung. Das Ganze sieht dann so aus:
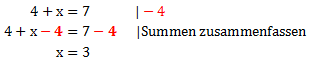
Wir haben also zunächst auf beiden Seiten 4 abgezogen. Diese haben wir am Ende notiert und im nächsten Schritt zusammengefasst. Links hat sich 4 und -4 gegeneinander aufgehoben. Rechts wurde aus 7 und -4 eine 3. Das Ergebnis ist damit x = 3. Wir setzen für x also 3 in die Ausgangsgleichung ein:
![]()
Natürlich ist dieses Beispiel relativ einfach. Es zeigt aber das Prinzip.
Beispiel 2: Gleichungen umformen
Hier ein weiteres Beispiel welches wir später bei den linearen Funktionen brauchen werden:
![]()
Die Ausgangsituation ist ähnlich, jedoch haben wir links nun noch einen Faktor vor dem x. wir möchten wieder, dass das x auf der linken Seite alleine steht. Wir müssen also die 4 und die 6 auf die andere Seite bringen. Nun müssen wir entscheiden, was wir als erstes tun. Wir könnten zum Beispiel als erstes durch 4 teilen um den Faktor vor dem x auf die andere Seite zu bekommen. Wir werden allerdings sehen, dass dies nicht der geschickteste Weg ist.

Hier ergibt sich ein Problem. Dadurch, dass wir durch 4 teilen, müssen wir natürlich auf beiden Seiten durch 4 teilen. Wegen der Punkt- vor Strichrechnung müssen wir links zunächst Klammern setzen, da wir ja die gesamte linke Seite durch 4 teilen müssen. Anschließend können wir diese Klammer wieder durch die Anwendung des erweiterten Distributivgesetzes auflösen. Am Ende kommen wir auf die Lösung x = 3.
Wir hätten natürlich auch zunächst minus 6 rechnen können. Dies ist wie wir sehen deutlich einfacher:

Hier sind die einzelnen Rechnungen deutlich einfacher und wir kommen schneller zum Ergebnis. Es ist also sinnvoll vorher zu überlegen wie man am besten vorgeht. In den meisten Fällen ist es sinnvoll zuerst die Strichrechnung durchzuführen und anschließend die Punktrechnung. Natürlich kommt man aber in allen Fällen auf dasselbe Ergebnis!
Das Ergebnis setzen wir noch einmal zur Kontrolle in die Ausgangsgleichung ein:
![]()
Wir sehen, dass unser Ergebnis richtig ist. Es kommt auf beiden Seiten dasselbe Ergebnis heraus.
Beispiel 3: Gleichungen umformen
![]()
In diesem Beispiel sollten wir erst einmal Ordnung schaffen. Die rechte Seite sollte erst einmal ausmultipliziert werden, damit das x nicht mehr innerhalb einer Klammer steht. Außerdem taucht das x hier mehrere Male auf. Wir müssen diese alle auf eine Seite bringen und zusammenfassen. Natürlich gibt es auch hier mehrere Möglichkeiten anzufangen. Wir beginnen mit dem Ausmultiplizieren und Zusammenfassen der rechten Seite:
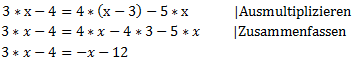
Jetzt haben wir die rechte Seite zusammengefasst und können mit dem Umformen weitermachen. Wir werden das x auf die linke Seite bringen. Alle anderen Teile auf die rechte. Wie oben empfohlen werden wir dabei zunächst die Strichrechnung vornehmen.

Die Lösung ist also x = -2. Zur Kontrolle setzen wir das Ergebnis noch einmal in die Ausgangsgleichung ein:
![]()
Wir sehen also, dass wir richtig gerechnet haben. Das Ergebnis ist auf beiden Seiten dasselbe.
