Bruchgleichungen
Was sind Bruchgleichungen?
Unter Bruchtermen versteht man eigentlich nur solche Terme mit Brüchen, bei denen die Variable auch im Nenner vorkommt.Man formt die Bruchgleichung so um, dass eine Gleichung ohne Bruchterme entsteht
Möchtet ihr direkt mit den Bruchgleichungen starten? Dann wollen wir euch an dieser Stelle noch bremsen, denn hier werden Vorkenntnisse im Bereich der Gleichungen und der Bruchrechnung vorausgesetzt.
Was ist eigentlich ein Bruchterm? Bei einem so genannten Bruchterm finden wir im Nenner eine Variable. (Der Nenner ist die Zahl unter dem Bruchstrich.) Stellen wir also eine Gleichung auf, in der mindestens ein Bruchterm enthalten ist, haben wir es mit einer Bruchgleichung zu tun. Um der Lösung einen Schritt näher zu kommen, werfen wir einen Blick auf die Nenner. In diesem Zusammenhang lässt sich die Definitionsmenge bestimmen.
Es lohnt sich auf jeden Fall, einen Blick auf die folgenden Themenbereiche zu werfen:
- Brüche kürzen und erweitern
- Brüche subtrahieren und addieren
- Brüche multiplizieren und dividieren
- Brüche gleichnamig machen
Vorsicht: Setze niemals einen Wert in der Variable ein, die in der Division durch Null endet.
In den meisten Fällen helfen euch Rechenbeispiele und Übungsaufgaben, um die Bruchgleichungen zu verstehen. Grundsätzlich ergeben sich in diesem Zusammenhang zwei unterschiedliche Lösungswege:
a) Äquivalenzverformungen und
b) lineare Gleichungen
Was bedeutet „Bruchgleichungen lösen?“
Bruchgleichungen lösen bedeutet ganz einfach:
- Definitionsmenge bestimmen
- Gleichung nach x auflösen
- Prüfen, ob das Ergebnis in der Definitionsmenge enthalten ist
Sicherlich fragt ihr euch “ Was tun, wenn ich im Bruch eine Variable habe z.B. „X“ ?
- Keine Sorge deswegen! Wir haben ja gesagt, dass eine Bruchgleichung dann vorliegt, wenn die Variable (z.B. x) im Nenner vorkommt.
- Die Gleichung wird so umgeformt, indem auf beiden Seiten die gleichen Rechenschritte durchgeführt werden: Es werden auf beiden Seiten immer die gleichen Umformungen vorgenommen!
- Zum Lösen einer Gleichung wird sie schrittweise so umgeformt, dass die gesuchte Variable allein und positiv auf einer Seite der Gleichung steht.
Merke: Jeder Bruch lässt sich beseitigen, indem ihr die Gleichung mit dem Nenner multipliziert.
Im Bereich der besonderen Lösungen, kann eine der Aufgaben und Bruchgleichungen keine Lösung ergeben, immer dann wenn sich zum Beispiel das berechnete Ergebnis nicht in der Definitionsmenge ergibt. In diesem Zusammenhang ist eine Lösung nicht definierbar.
Im Gegenzug ist es möglich, dass unendlich viele Lösungen in Betracht kommen. Das ist immer dann der Fall, wenn auf beiden Seiten derselbe Term erscheint. Dann wäre die Definitionsmenge für alle Variablen erfüllt.

Nun wollen wir gemeinsam einen Beispiel rechnen!

Unser Lernvideo zu : Bruchgleichungen
Wir berechnen gemeinsam noch ein Beispiel!
![]()
- Die Terme der Gleichung sind an den Nullstellen der Nenner nicht definiert.Für die gesuchte Größe x müssen wir also von Anfang an die Werte 1 und –1 ausschließen. Unsere Definitionsmenge ist daher.
![]()
Wir bringen alles auf eine Seite
![]()
- und addieren die Brüche (Zur Erinnerung: den Hauptnenner aller Brüche bestimmen, jeden einzelnen Bruch auf den Hauptnenner erweitern.)
![]()
- Beide Seiten der Gleichung mit dem Hauptnenner multiplizieren (das dürfen wir, da der Hauptnenner auf dem Grundmenge von Null verschieden ist!) liefert
![]()
- Damit haben wir die gesuchte Größe aus dem Nenner weggeschafft. In diesem Fall sehen wir, das nur noch eine quadratische Gleichung zu lösen ist, wobei wir aber nicht an beliebigen Lösungen interessiert sind, sondern nur an solchen aus der Definitionsmenge D.
- Lösen der quadratischen Gleichung indem man sie (durch Ausmultiplizieren und Ordnen nach den Potenzen von x) auf Normalform bringt
![]()
p = –5 und q = 6 abliest und in die pq-Formel einsetzt
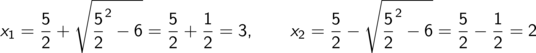
Sowohl 2 als auch 3 liegen in der Grundmenge, und sind somit auch Lösungen der Bruchgleichung.

