Rechnen mit Variablen
Zwar haben wir in den vorhergehenden Kapiteln schon ab und zu mit Variablen gearbeitet, wirklich wichtig wird es aber erst jetzt. Wir geben daher an dieser Stelle eine kleine Einführung über das Rechnen mit Variablen. Grundsätzlich ist eine Variable ein Platzhalter, der eine beliebige Zahl annehmen kann.
Variablen werden mit Buchstaben dargestellt. Häufig sieht man das x als Variable. Man kann jedoch alle Buchstaben als Variable benutzen. So kann zum Beispiel a, b, k, l usw. als Variable verwendet werden. Nicht zu verwechseln sind Variablen mit Konstanten. Diese haben einen festen Wert.
Unser Lernvideo zu : Rechnen mit Variablen
Schreibweise
Das „Malzeichen“ können wir vor oder nach Variablen weglassen. Beispiele:
![]()
Die 1 wird in den meisten Fällen auch weglassen, da die Multiplikation mit Eins den Wert der Zahl nicht verändert.
![]()
Zusammenfassen von Variablen
Variablen können in bestimmten Fällen zusammen gerechnet werden.
Addieren
Summanden können addiert werden, wenn sowohl die Variable als auch die Hochzahl der Variable gleich ist. Dabei wird der Zahlenwert addiert und die Variable unverändert beibehalten.
z.B.: x + 2x = 3x
4x + 3x = 7x
x² + 3x² = 4x² (die Hochzahl änder sich nicht!)
Sind verschiedene Variablen vorhanden, muss man beachten, dass nur gleichwertige addiert werden dürfen.
z.B.: x + a + 3x + 4a = 4x + 5a
a + b + a + 2b + a = 3a + 2b
2x + x + x² + 4x² = 3x + 5x²
x² + a + 2x² + b + a = 3x² + 2a + b
Subtrahieren
Es gelten die gleichen Regeln wie beim Addieren. Nur gleiche Variablen dürfen subtrahiert werden!
z.B.: 3x – x = 2x
4x – 2a – 2x = 2x – 2a
Addieren und subtrahieren gemischt
Dabei markiert man sich zunächst die zusammen passenden Variablen und die Vorzeichen, ob es Plus oder Minus ist. Und zählt erst dann die einzelnen Variablen zusammen bzw. zieht sie von einander ab.
z.B.: 4x + 3x² + a – x + x² – 3a = 3x + 4x² – 2a
Multiplizieren gleicher Variablen
Es kommt häufig vor, dass wir gleiche Variablen multiplizieren:
![]()
Das ² bedeutet „hoch 2“ und wird auch als Quadrat bezeichnet. Man bezeichnet diese Zahl als Exponenten. Genau erklärt wird dies in einem späteren Kapitel. Es bedeutet, dass man x mal x rechnen muss. Bei einem ³ muss man x mal x mal x rechnen. Die Zahl gibt also an wie oft man x multiplizieren muss.
![]()
Wenn nun x mehrere Male in einer Gleichung vorkommt erleichtert einem diese Schreibweise viel Arbeit.
Beispiel
![]()
Dieses nennt man auch quadratische Gleichung, da das x zum Quadrat genommen wird.
Aufpassen muss man wenn eine Variable mit unterschiedlichem Exponenten vorkommen. Bei einer Addition kann man Variablen nur zusammenfassen, wenn sie den selben Exponenten besitzen.
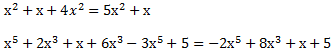
Diese beiden Beispiele können nicht weiter zusammengefasst werden, da die Variable x nur noch mit unterschiedlichem Exponenten auftritt.
Unterschiedliche Variablen
Wenn in einer Gleichung unterschiedliche Variablen zusammenkommen können wir die unterschiedlichen Variablen nicht zusammenfassen. Nur die Teile mit gleichen Variablen können zusammengefasst werden:
![]()
Weiter kann man diesen Term nicht zusammenfassen, da es sich um unterschiedliche Variablen handelt.
