Ungleichungen
Was sind Ungleichungen?
Eine Ungleichung verbindet zwei Terme mit einem der folgenden Rechenoperationen
< (Kleinerzeichen),
≤ (Kleinergleichzeichen),
> (Größerzeichen) oder
≥ (Größergleichzeichen)
Vorgehensweise beim Lösen einer Ungleichung
- Auf beiden Seiten der Ungleichung eine Zahl addieren/subtrahieren
- Beide Seiten der Ungleichung mit einer Zahl multiplizieren bzw. durch eine Zahl dividieren
- Wichtig: Multipliziert/dividiert man die Ungleichung mit einer negativen Zahl dreht sich das Ungleichheitszeichen um!
- Vorsicht: Potenzieren, Wurzelziehen und Quadrieren sind keine Äquivalenzumformungen!
Damit Ihr den Begriff “ Ungleichung“ besser verstehen könnt; nehmen wir den Beispiel mit dem Vergleich der Größen zweier Menschen.
Stellt euch vor, ihr seit 1,60m groß und euer Klassenkammerad ist 1,75 m groß. Wir können nun sagen, dass euer Klassenkamerad größer ist als euch. Dieses Verhältnis wird in der Mathematik mit der Logischen Ausdruck wieder gegeben. Und zwar folgendermaßen:
1,75 > 1,60 ( größer als)
1,75 < 1,60 (kleiner als)
Kommen wir auf unser Thema wieder zurück! Wir berechnen gemeinsam einen Beispiel.
2x – 3 ≥ x + 1 | – x zu beiden Seiten –x addieren (d.h. x subtrahieren)
x – 3 ≥ 1 | + 3 zu beiden Seiten 3 addieren
x ≥ 4
L = { x | x ≥ 4 }
Wörtlich besagt die Lösungsmenge: Die Lösungsmenge besteht aus allen reellen Zahlen, die größer-gleich 4 sind. (d.h. größer als 4 oder gleich 4)
Nehmen wir noch ein Beispiel zur veranschaulich. Berechnet werden soll folgende Ungleichung 2x – 5 > 2
Wir berechnen wieder mit der Äqualenzumformung schrittweise:
2x – 5 > 2 | + 5
2x – 5 + 5 > 2 + 5
2x + 0 > 2 + 5
2x > 7 | : 2
x > 3,5
Die Ungleichung ist somit für alle x Werte erfüllt, die größer als 3,5 sind. Beispiel x = 3,6 oder x = 4.
Wir machen die Probe für x = 4:
2x – 5 > 2 | x = 4
2·4 – 5 > 2
8 – 5 > 2
3 > 2
Also ist diese Aussage ist wahr!
Unser Lernvideo zu : Ungleichungen
Wichtig ist dabei auch die Intervallschreibweise. Wenn ich richtig berechnet aber die Intervallschreibweise falsch aufschreibt, ist das Ergebnis Falsch! Damit euch solche Fehler nicht auftreten, hier eine kurze Einleitung
Wir machen das ganze mit dem Beispiel 2 und 5
a) 
beschreibt die Menge aller Zahlen von einschließlich 2 bis ebenfalls einschließlich 5. In anderen Worten:Die Zahlen von mindestens 2 bis höchstens 5
D.h. beide Ränder sind jeweils eingeschlossen.
b) 
beschreibt die Menge aller Zahlen von einschließlich 2 bis ausgeschlossen 5. Einfacher gesagt:Die Zahl 2 ist noch in der Menge enthalten, die Zahl 5 jedoch nicht. Zahlen wie z.B. 4,9999 oder 4,9999999 liegen aber noch innerhalb dieser Menge.
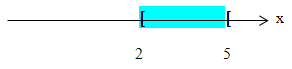
c) 
beschreibt die Menge aller Zahlen von ausgeschlossen 2 aber eingeschlossen 5. Das bedeutet, dass die Zahl 2 nicht mehr in dieser Menge liegt, die Zahl 5 aber schon noch. Zahlen wie z.B. 2,000001 oder 2,0001 liegen dagegen auch noch darin.
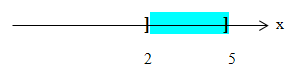
d) 
beschreibt die Menge aller Zahlen von ausgeschlossen 2 bis ebenfalls ausgeschlossen 5, da beide Klammern nach außen, also von den Zahlen 2 und 5 weg gerichtet sind. Diese Menge enthält also nur Zahlen, die größer als 2 aber auch gleichzeitig kleiner als 5 sind. Zahlen wie z.B. 2,000001 oder 4,99999 liegen aber noch innerhalb.
e) 
beschreibt die Menge aller Zahlen, die kleiner oder gleich 2 sind. D.h. die Grenze 2 ist noch eingeschlossen, da die eckige Klammer nach innen zur Zahl 2 hin gerichtet ist. Die Klammer bei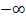 
(Sprich:„Minus-Unendlich“) zeigt nach außen;da Minus-Unendlich keine normale Zahl ist, wird es immer ausgeschlossen.
f) 
beschreibt die Menge aller Zahlen, die kleiner als 2 sind. Die Grenze 2 ist hier ausgeschlossen, da die eckige Klammer von der Zahl 2 weg gerichtet ist. Zahlen wie z.B. 1,99999 oder 1,99999999 liegen aber noch innerhalb dieser Menge.
g) 
beschreibt die Menge aller Zahlen, die größer oder gleich 2 sind. Die Grenze 2 ist noch eingeschlossen, da die eckige Klammer nach innen, also zur 2 hin gerichtet ist. Die Klammer bei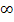 
(Sprich:„Unendlich“) zeigt nach außen;da Unendlich – genauso wie Minus-Unendlich – keine echte Zahl ist, wird es immer ausgeschlossen.
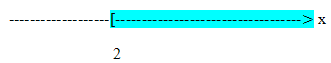
h) 
beschreibt die Menge aller Zahlen, die größer als 2 sind. Die Grenze 2 ist hier ausgeschlossen, da die eckige Klammer von der Zahl 2 weg gerichtet ist. Zahlen wie z.B. 2,0000001 oder 2,00001 liegen aber noch innerhalb dieser Menge. Unendlich ist natürlich, wie vorher bereits erläutert, ausgeschlossen.
