Distributivgesetz
Das Distributivgesetz zeigt uns wie man Klammern ausmultiplizieren kann. Dies ist also ein Verfahren um Klammern aufzulösen (auszumulitplizieren). Die Voraussetzung dafür ist, dass vor oder nach der Klammer ein Mal- oder Geteiltzeichen steht und in der Klammer Plus- oder Minuszeichen.
Mit Hilfe des Distributivgesetzes können wir diese Klammern auflösen. Natürlich könnten wir auch wie unter „Rechenregeln“ beschrieben zuerst die Klammern ausrechnen und anschließend die Multiplikation durchführen, in vielen Fällen ist es aber einfacher oder notwendig das Distributivgesetz anzuwenden.
Unser Lernvideo zu : Distributivgesetz
Addition
Für die Addition funktioniert das Ganze folgendermaßen:
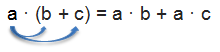
Wir multiplizieren also a mit b und addieren dann das Produkt aus a und c. Dadurch fällt die Klammer weg.
Ein Zahlenbeispiel für das ausmultiplizieren:
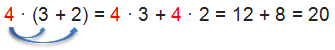
Eine andere Darstellung für das Gleiche Beispiel:
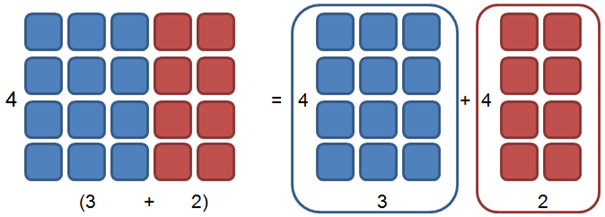
Subtraktion
Das Gleiche geht auch für die Subtraktion. Dann sieht es folgendermaßen aus:
![]()
Die Multiplikation bleibt also die Gleiche. Der einzige Unterschied ist, dass zwischen den Teilen ein Minuszeichen steht.
Beispiel

Vertauschen der Faktoren
Da die Multiplikation kommutativ ist (man also die Faktoren vertauschen darf), können wir bei den gezeigten Beispielen auch die Faktoren vertauschen. Das Malzeichen steht dann also hinter der Klammer:
![]()

Division
Bisher haben wir hier nur die Multiplikation in Verbindung mit der Addition und Subtraktion betrachtet. Man kann das Distributivgesetz jedoch auch mit der Division anwenden. Damit wir das Gesetz bei der Division anwenden dürfen, muss nach der Klammer ein Geteiltzeichen stehen und in der Klammer Minus- oder Pluszeichen.
Das Distributivgesetz für die Division gilt nicht bei einem Geteiltzeichen vor der Klammer.
![]()
![]()
![]()
Beispiele:
![]()
![]()
Drei oder mehr Summanden
Das Distributivgesetz funktioniert aber nicht nur mit zwei Summanden innerhalb einer Klammer, sondern auch wenn in der Klammer 3 oder mehr Summanden stehen. Das Vorgehen ist dasselbe.
Beispiel
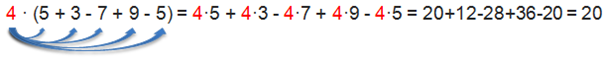
Natürlich hätten wir in diesem Beispiel auch erst die Klammer ausrechnen und das Ergebnis dann mit 4 multiplizieren können:
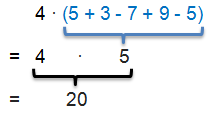
Das Ergebnis ist in beiden Fällen 20. Welchen Weg man nimmt, ist Geschmackssache. Für spätere Themen ist es aber sehr wichtig, beide Wege zu kennen.
Rechenvorteile
Auch mit Hilfe des Distributivgesetzes kann man sich Rechenvorteile verschaffen. Hierdurch können große Faktoren in kleinere zerlegen werden und man erhält mehrere einfachere Teilrechnungen:
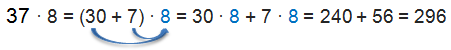
Defintionen rund um das Distributivgesetz
Ungleichungen = Mit Ungleichungen werden Größenvergleiche formuliert und untersucht
Rechengesetze = Rechengesetze sind Regel, die angibt, wie man mathematische Operationen äquivalent umformen darf.
Interessante Fragen und Antworten zu Distributivgesetz
Wie das Distributivgesetz mit 2 Klammern geht weiss ich, doch wie geht es mit 3 Klammern? |
| Das Distributivgesetz ist sehr einfach, wenn man weiß wie es geht!Um das Gesetz zu erklären arbeiten wir mit einem Beispiel:
(1+2) x (3+4) x (5+6) = Im ersten Schritt lösen wir nun die ersten zwei Klammern auf, ganz nach der Vorgehensweise zuerst von links nach rechts. Das heißt: (1×3 + 1×4 + 2×3 + 2×4) x ( 5+6) = Um die einzelnen Zahlen zu vereinfachen rechnen wir jetzt die Malsummen aus der Klammer nach der Regel Punkt vor Strich aus: Das heißt: (3 + 4 + 6 + 8) x (5+6) = Im nächsten Schritt multiplizieren wir die beiden Klammern wieder miteinander: Das heißt: 3×5 + 3×6 + 4×5 + 4×6 + 6×5 + 6×6 + 8×5 + 8×6 = Was jetzt kommt, ist super einfach, da wir einfach nach Punkt vor Strich vorgehen: 15 + 18 + 20 + 24 + 30 + 36 + 40 + 48 = Im letzten Schritt rechnen wir dann einfach alle Zahlen zusammen und erhalten die Endlösung: 231 Um das ganze als Formel darzustellen nutzen wir diese Schreibweise und gehen wie im Beispiel vor: (a+b) x (c+d) x (e+f) = |
Wie formt man im Distributivgesetz Terme um? |
| Als erstes muss die Vorzeichenregel berücksichtigt werden, wenn eine Klammer mit einer Zahl multipliziert oder dividiert werden soll. Werden zwei Zahlen mit gleichen Vorzeichen multipliziert oder dividiert, ist das Ergebnis immer eine positive Zahl. Bei zwei verschiedenen Vorzeichen kommt als Ergebnis eine negative Zahl heraus. Soll eine Klammer mit einer Zahl multipliziert oder dividiert werden, muss man jede Zahl in der Klammer mit der Zahl dividieren oder multiplizieren.Beispiele:
(8 + 4) : 2 = 8 : 2 + 4 : 2 = 4 + 2 = 6 Wenn zwei Terme einen gemeinsamen Faktor teilen, kann man diesen ausklammern. Beispiel: 4 · 3 + 5 · 3 = 3 · (4 + 5) = 3 · 4 + 3 · 5 = 12 + 15 = 27 |
Wie formt man im Distributivgesetz Terme um? |
| Terme, die umgeformt werden sollen, allerdings noch in Klammern stehen, lassen sich erst nach einem Zwischenschritt gut umformen. Hierzu wird wie gewohnt zunächst das Distributivgesetz angewandt.Beispiel: a + 2*(2b + 3a)
Zwar kommt a innerhalb und außerhalb der Klammer vor, es kann jedoch nicht ohne weiteres umgeformt werden. Nach dem Ausklammern wird dies dafür umso leichter. a + 2*(2b + 3a) = Dies funktioniert auch mit komplizierteren Rechnungen. Beispiel: x + 3*(x + 2y – 2z) – 2z = Die Umformung der Terme erfolgt erst zum Schluss oder als Zwischenschritt nach der Anwendung des Distributivgesetzes. |
Wie kann ich mir das Distributivgesetz merken? |
| Sich das Distributivgesetz zu merken, ist eigentlich gar nicht so schwierig. „Distribuere“ kommt aus dem Lateinischen und bedeutet „verteilen“. Genau das macht man dabei. Man verteilt alles, was in einer Klammer steht mit dem, was außerhalb der Klammer steht. Merken muss man sich hier, dass dies nur dann gilt, wenn die Klammer und alles, was darin steht, mit einer Zahl, einem Term oder einer weiteren Klammer multipliziert oder dividiert wird. Ist das der Fall, wird alles, was in der Klammer steht nacheinander mit allem multipliziert oder dividiert, was außerhalb der Klammer steht. Geht man hier Schritt für Schritt vor, ist das auch ganz einfach und übersichtlich.Es kann aber auch helfen, wenn man sich ein Beispiel wie a*(b + c) = a*b + a*c merkt. Daran kann man wunderbar erkennen, wie das Distributivgesetz funktioniert und wie man vorgehen muss. Hat man das verstanden, ist es ein Leichtes, sich die Regel zu merken.
Alternativ kann man sich aber auch einfach vorstellen, dass man Bonbons an Freunde verteilt. Dabei wird alles, was in der Bonbontüte (Klammer) ist, an alle Freunde verteilt. Am Ende sind alle Bonbons aus der Tüte raus (Klammer aufgelöst) und alle Freunden haben was zu Naschen. |
Wie wendet man das Distributivgesetz bei 3 Klammern mit Quatrat an? |
| Das Distributivgesetz beschreibt, wie man Klammern nach mathematischen Regeln korrekt auflöst bzw. wie man eine Summe durch Ausklammern in ein Produkt verwandelt. Das Distributivgesetz gehört zu den grundlegenden Regeln der Algebra. Bei drei Klammern mit Quadrat haben wir beispielsweise eine Formel folgender Art vorliegen: (x+1)(x-2)(x-1)^2. Als erstes muss man das Quadrat in ein Produkt umwandeln, also: (x+1)(x-2)(x-1)(x-1). Danach werden sämtliche Klammern aufgelöst durch Ausmultiplizieren der einzelnen Elemente mit jedem. Hilfreich kann es sein, zuerst die ersten beiden Klammern auszumultiplizieren und im gleichen Schritt auch die letzten beiden, sodass wir folgendes Zwischenergebnis erhalten: (x²-x-2)(x²-2x+1). Im nächsten Schritt wird dann jedes Element der ersten mit jedem Element der zweiten Klammer multipliziert unter Beachtung der Vorzeichen, und man erhält: x^4 – 2x^3 +x² – x^3 + 2x² – x – 2x² + 4x -2. Im letzten Schritt braucht man nur noch entsprechend zu addieren bzw. subtrahieren, und man erhält das Endergebnis: x^4 – 3x^3 + x² + 3x -2. |
