Rechenregeln
Punkt- vor Strichrechnung
Eine der wichtigsten Rechenregeln ist, im Regelfall immer alle Punktrechnungen vor den Strichrechnungen durchzuführen. Die Punktrechnung umfasst dabei die Multiplikation und die Division. Auch die Potenz gehört dazu, da sie eine kurzschreibweise für die Multiplikation ist (2³ = 2 · 2 · 2). Zu der Strichrechnung gehören die Subtraktion und die Addition.
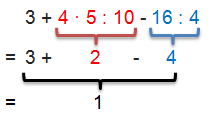
Beispiel 3 + 4 · 5 : 10 – 16 : 4
Bei dieser Rechnung können wir nicht einfach von links nach rechts vorgehen, da wir die Punktrechnung (also alle Multiplikationen und Divisionen) vor der Strichrechnung (Addition und Subtraktion) durchführen müssen.
Wir nehmen uns also als erstes den Teil 4 · 5 : 10 vor. Hier rechnen wir zunächst 4 · 5 = 20 und anschließend 20 : 10 = 2.
Als nächstes müssen wir 16 : 4 = 4 berechnen. Nun haben wir alle Punktrechnungen durchgeführt. Das Zwischenergebnis ist: 3 + 2 – 4.
Da in der Rechnung keine Punktrechnung mehr vorhanden ist, können wir die Strichrechnung durchführen: 3 + 2 – 4 = 1.
Unser Lernvideo zu : Rechenregeln
Klammerregeln
Ebenfalls wichtig ist der Umgang mit Klammern. Klammer setzt man um zu erreichen, dass das Innere der Klammern zuerst gerechnet wird. Auch innerhalb einer Klammer gilt natürlich Punkt- vor Strichrechnung.
Beispiel 1
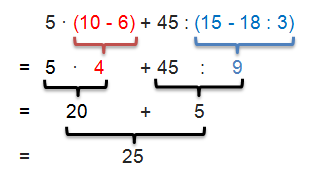
Wir müssen hier zuerst die Klammern berechnen. 10 – 6 = 4 und 15 – 18 : 3 = 9 (Punkt vor Strichrechnung beachten). Jetzt haben wir alle Klammern aufgelöst und können den Rest der Aufgabe lösen: 5 · 4 + 45 : 9. Auch hierbei wird zunächst die Punktrechnung vorgenommen, also 5 · 4 = 20 und 45 : 9 = 5. Als letztes wird die Addition von 20 und 5 durchgeführt: 20 + 5 = 25.
Beispiel 2
Ein bisschen schwieriger wird es, wenn die Aufgabe mehrere geschachtelte Klammern enthält.
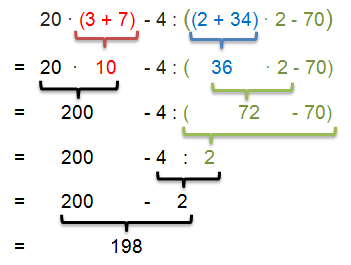
Wir müssen uns bei diesem Beispiel von innen nach außen arbeiten. Die innerste Klammer muss also zuerst berechnet werden, anschließend berechnen wir die äußere Klammer. Wenn, wie in diesem Beispiel, Klammern ineinander verschachtelt sind, kann man für die äußeren Klammern alternativ auch eckige Klammern verwenden, damit diese besser zu unterscheiden sind. Die Schreibweise wäre dann: 20 · (3 + 7) – 4 : [(2 + 34) · 3 – 2]. Welche Version man letztendlich verwendet, ist dabei nur Geschmackssache.
Klammern mit Plus- oder Minuszeichen auflösen
Klammern, vor denen ein Pluszeichen steht, können sehr einfach aufgelöst werden. Wir können die Klammern in diesem Fall einfach weglassen. Warum dies geht und welches Gesetz dahinter steht, lernt ihr im Abschnitt Kommutativgesetz.
Beispiel 1
5 + (30 + 6) = 5 + 30 + 6 = 41
Bei einem Minuszeichen vor der Klammer, ist es nicht ganz so einfach. Um die Klammer aufzulösen, müssen wir in diesem Fall alle Plus- und Minuszeichen innerhalb der Klammer umkehren. Aus Plus wird also Minus und aus Minus wird Plus. Wenn die erste Zahl in der Klammer kein Vorzeichen besitzt, können wir uns an dieser Stelle ein Plus denken, welches dann zu einem Minus wird. Das Gleiche passiert bei der Multiplikation von negativen Zahlen (siehe Kapitel „schriftliches Multiplizieren“). Immer wenn zwei Minuszeichen aufeinander treffen und hintereinander stehen würden, wird daraus ein Pluszeichen.
Beispiel 2
30 – (8 – 6 + 3 – 10 + 3) = 30 – 8 + 6 – 3 + 10 – 3 = 32
15 – (-3 + 8) = 15 + 3 – 8 = 10
Klammern mit Mal- oder Geteiltzeichen auflösen
Klammern vor oder hinter denen ein Mal- oder Geteiltzeichen steht, können mit Hilfe des Distributivgesetzes aufgelöst werden. Da dies ein wichtiges mathematisches Gesetz ist, haben wir es in einem eigenen Kapitel beschrieben.
