Schriftliches Dividieren
Grundsätzlich steigen wir mit dem Dividieren schon in der 4. Klasse ein. Wobei man beim Kopfrechnen gerade bei großen Zahlen schnell an seine Grenzen stößt. Ein Grund mehr, eine der geläufigsten Methoden des schriftlichen Dividierens einzuüben.
Eine der Grundrechenarten ist die Division. Wir stellen hier ein Verfahren vor, mit dem man zwei Zahlen schriftlich dividieren kann, und verdeutlichen das Verfahren anhand mehrerer Beispiele. Zunächst beginnen wir mit einem einfachen Beispiel, an dem man das Prinzip erkennen kann, und erläutern daraufhin weitere Möglichkeiten dieses Verfahrens. Insbesondere häufiges Üben führt zu einer Verinnerlichung der einzelnen Rechenschritte. Schon bald fallen dir die Schritte bis hin zum Ergebnis leicht. Zudem kommen die Verfahren zum schriftlichen Dividieren auch in Sachaufgaben zur Anwendung.
Die Division ordnen wir den Grundaufgaben in der Mathematik zu. Schlussendlich ist es nichts weiter als die Umkehrung der Multiplikation. Auch bei der Division gibt es einige Fachbegriffe. Die Zahl, durch die geteilt wird, heißt Dividend und die Zahl, mit der geteilt wird, nennt man Divisor. Das Ergebnis beider Zahlen ist der Quotient. Die Zeichen für die Division sind „:“, „÷“ bzw. „/“. Welches man davon wählt ist Geschmackssache, die Bedeutung ist immer dieselbe.
Dividend : Divisor = Quotient
Jeder, der multiplizieren kann, wird auch das Dividieren schnell beherrschen. Teilen wir also den Dividenden 20 durch den Divisor 5 erhalten wir als Quotienten 4. Anders ausgedrückt: Die 5 passt 4 Mal in die 20 oder teilen wir 20 in 5 Pakete, sind in jedem Paket 4 enthalten. Am deutlichsten wird dies mit dem Kuchenmodell, das wohl fast jeder schon einmal auf der Tafel gesehen hat. Doch nicht jede Rechnung geht so einfach aus, wie unser oberes Rechenbeispiel.
Ein häufiges Problem beim Teilen zweier Zahlen wie 4 : 5 ist der auftretende Rest, durch den man in den Bereich der Kommazahlen gelangt. Mit dem hier vorgestellten Verfahren können wir auch das Ergebnis einer Division bestimmen, bei welcher der Dividend kleiner ist als der Divisor.
Die Division ist vermutlich die schwierigste Grundrechenart. Um eine schriftliche Division großer Zahlen durchführen zu können, benötigt man sichere Kenntnisse über Multiplikation und Subtraktion.
Die wichtigsten Eigenarten bei der Division
Um keine Probleme mit dem Dividieren zu bekommen, solltet ihr nicht nur die einzelnen Rechenschritte beachten, sondern auch die Eigenarten im Kopf behalten. Wir haben nun gelernt, dass es sich bei der Division um die Umkehrung der Multiplikation handelt. Außerdem besagt das Kommutativgesetz, dass sich Dividend und Divisor nicht einfach umdrehen lassen. Das würde zu einem unterschiedlichen Ergebnis führen. Das scheint einer der wichtigsten Unterschiede zu den anderen Grundrechenarten, wieder Addition und der Multiplikation, zu sein.
Eine weitere, wichtige Eigenart ist das schriftliche Dividieren mit 0. So darf der Dividend zum Beispiel den Wert 0 annehmen, wohingegen der Divisor niemals 0 sein darf. Ist dies dennoch der Fall, ist das Ergebnis: nicht lösbar. Zumeist können wir die Division mit kleinen Dividenden noch im Kopf ausrechnen. Steigt diese Zahl in der Höhe, kommen wir zum schriftlichen Dividieren.
Rechner Schriftliches Dividieren
Unser Lernvideo zu : Schriftliches Dividieren
1. Beispiel: 1379 : 7 (Geteilt rechnen)
Zunächst ist die Aufgabe auf Karopapier aufzutragen. Wir schreiben die Zahlen dabei nebeneinander, getrennt durch das Geteiltzeichen und gefolgt von einem Gleichzeichen. Dadrunter benötigen wir einige Zeilen Platz für die kommenden Rechnungen.

Wir beginnen mit der ersten Stelle der ersten Zahl (dem Dividend 1379). Hier steht vorne eine 1. Da wir durch 7 teilen, prüfen wir, wie oft die Zahl 7 (der Divisor) in die 1 passt (1 : 7 = 0). Das Ergebnis ist 0, da die Zahl 7 kein ganzes Mal in die 1 passt (Kommastellen interessieren uns an dieser Stelle nicht). Weil das Ergebnis 0 ist, müssen wir auch noch die nächste Stelle dazunehmen (die 3).
Wir prüfen nun also wie oft die Zahl 7 in die Zahl 13 passt (13 : 7 = 1,…). Die 7 passt ein ganzes Mal in die 13. Das Ergebnis ist also 1. Wir notieren dieses Ergebnis rechts neben dem Gleichzeichen. Die 1 ist also die erste Stelle unseres Ergebnisses. Außerdem müssen wir unter der 13 das Ergebnis der Multiplikation von 1 und 7 notieren (1 · 7 = 7). Wir schreiben die Zahlen dabei rechtsbündig untereinander, sodass wie bei der schriftlichen Subtraktion die Einer und Zehner der beiden Zahlen untereinander stehen.

Jetzt können wir die Subtraktion durchführen. Wir schreiben dafür noch das Minuszeichen links neben die zweite Zeile und machen einen Strich unter die beiden Zahlen. Bei der Subtraktion gehen wir genau wie im Kapitel “Schritliches Subtrahieren” beschrieben vor. Das Ergebnis ist 6.

Wir gehen jetzt von der 6 aus (dem Ergebnis der Subtraktion) und ziehen die nächste Stelle des Dividenden herunter (die 7). Wir erhalten also die Zahl 67. Jetzt wiederholt sich das Vorgehen. Wir prüfen, wie oft die 7 in die 67 passt (67 : 7 = 9,…). Wieder interessieren uns die Kommastellen der Division nicht und wir notieren die 9 als Ergebnis neben der 1. Unter der 67 notieren wir das Ergebnis der Multiplikation von 9 und 7 (9 · 7 = 63). Dabei achten wir darauf, dass Einer uns Zehner untereinander stehen. Jetzt führen wir wieder eine Subtraktion durch, rechnen also 67 – 63 = 4.
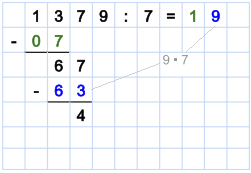
Als nächstes ziehen wir wieder die nächste Stelle der ersten Zahl herunter (die 9). Diese schreiben wir neben die 4 und prüfen wieder, wie oft die 7 in die 49 passt (49 : 7 = 7). Die 7 schreiben wir als nächste Stelle zum Ergebnis, rechnen 7 · 7 = 49 und schreiben das Ergebnis unter die 49. Als Ergebnis der Division erhalten wir 0.
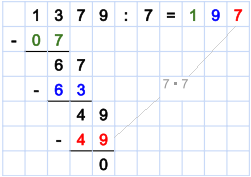
Da wir nun am Ende der Zahl 1379 angekommen sind, können wir keine weitere Stelle mehr runterziehen. Wir sind also am Ende der Division angekommen. Ein Problem ergibt sich aber, wenn bei der letzten Division eine Zahl größer als 0 rausgekommen wäre. Diese Zahl gibt den Rest der Division an. 1379 ist also ohne Rest durch 7 teilbar. Das Ergebnis ist 197. Im nächsten Beispiel zeigen wir, wie man vorgeht, wenn bei der letzten Subtraktion ein Rest übrig bleibt und man die Nachkommastellen berechnen möchte.
2. Beispiel 45 : 8 (Geteilt rechnen)
An diesem Beispiel zeigen wir, wie man vorgeht, wenn das Ergebnis Kommastellen besitzt. Wir notieren die Aufgabe zunächst folgendermaßen:
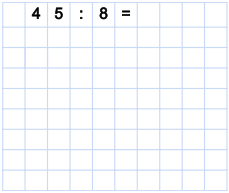
Wir beginnen mit der ersten Stelle des Dividenden (der 4). Wir prüfen, wie oft die 8 in die 4 passt (4 : 8 = 0). Da die 8 kein Mal in die 4 passt, nehmen wir die nächste Stelle dazu (45 : 8 = 5). Wir notieren also die 5 als erste Stelle des Ergebnisses und multiplizieren 5 mit 8 (5 · 8 = 40). Die 40 schreiben wir unter die 45 und führen die Subtraktion durch (45 – 40 = 5).

Wir müssten nun die nächste Stelle vom Dividenden runterziehen. Der Dividend hat aber keine weitere Stelle. Wir sind also eigentlich fertig mit der Division. Das Ergebnis ist 45 : 8 = 5, der Rest beträgt also 5. Meistens wollen wir es aber genauer wissen und die Nachkommastellen genau berechnen. Wir helfen uns also mit einem Trick. Wir denken uns hinter der Zahl 45 noch beliebig viele Nullen (45 = 45,00000000).
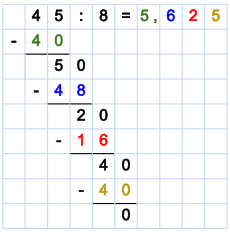
Wir notieren hinter dem aktuellen Ergebnis ein Komma (dies macht man immer, sobald man beim Dividend eine Zahl hinter dem Komma runterzieht), ziehen uns eine 0 runter und rechnen mit dieser weiter. So erhalten wir die Zahl 50. Wir teilen 50 durch 8 und erhalten 6 (50 : 8 = 6), was als Ergebnis notiert wird. Das Vorgehen ist also wie zuvor, nur ziehen wir jetzt noch Nullen runter (wenn der Dividend Nachkommastellen hätte, müssten wir allerdings zunächst diese runterziehen).
Wir wiederholen diese Schritte so lange, bis wir bei der Subtraktion eine 0 erhalten. Sobald wir eine Null erhalten, sind wir fertig mit der Rechnung und haben diese Aufgabe komplett gelöst. Das Ergebnis ist 5,625.
3. Beispiel 4 : 3 (Geteilt rechnen)
Eine Besonderheit ergibt sich bei der Aufgabe 4 geteilt durch 3. Wenn wir diese beiden Zahlen durch einander Teilen, gehen wir zunächst genauso vor wie beim vorhergehenden Beispiel.
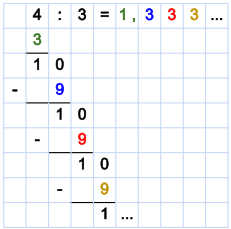
Das Problem ist allerdings, dass das Ergebnis der Subtraktion niemals Null ergibt. Wir können in diesem Fall die Rechnung abbrechen, sobald wir merken, dass sich ein Teilschritt wiederholt. Wir merken bei diesem Beispiel, dass wir immer wieder einen Rest von 1 erhalten. Wir könnten jetzt noch endlos weitermachen, würden aber niemals zu einem Ende kommen.
Wir können die Rechnung also abbrechen und den Teil, der sich wiederholt, als sogenannte Periode schreiben. Bei der Rechnung 4 : 3 wiederholt sich nur die 3. Deshalb schreiben wir als Ergebnis 1,3. Der Überstrich über der 3 gibt dabei an, dass sich der Teil unter dem Strich immer wiederholt.
Tipps und Tricks zum Kopfrechnen
Wenn man eine Division großer Zahlen im Kopf durchführen soll, wird es schnell schwierig. Es gibt zwei Vorgehensweisen. Zum einen können die oben genannten Schritte komplett im Kopf durchgeführt werden. Hierbei ist es am Anfang schwer den Überblick zu behalten und sich das Ergebnis und die Zwischenschritte zu merken. Mit ein bisschen Übung wird man hiermit aber immer größere Zahlen im Kopf rechnen können.
Die andere Möglichkeit besteht darin, die Aufgabe aufzuteilen. Und zwar so, dass die einzelnen Teile möglichst leicht zu Rechnen sind. Wenn man zum Beispiel 396 : 6 im Kopf rechnen möchte. Sollte man sich zunächst an das Ergebnis annähren, indem man 6 mit 10, 20, 30 usw. Multipliziert und jedesmal überprüft, ob das Ergebnis noch kleiner ist als 396, wodurch man auf auf 6 · 60 = 360 kommt.
Nun zieht man 360 von 396 ab. 396 – 360 = 36.
Man merkt sich die 60, rechnet nun 36 : 6 = 6 im Kopf und addiert anschließend die 60 (60 + 6 = 66). Damit hat man das Endergebnis: 396 : 6 = 66.
Bei noch größeren Zahlen sollte man zusätzlich mit den Hundertern rechnen.
3225 : 5
-
Schritt: 5 · 600 = 3000
-
Schritt: 3225 – 3000 = 225
-
Schritt: 5 · 40 = 200
-
Schritt: 225 – 200 = 25
-
Schritt: 5 · 5 = 25
Die Fett geschriebenen Zahlen muss man sich jeweils merken und am Ende addieren. Das Ergebnis ist also 600 + 40 + 5 = 645.
Aufgaben mit Lösungen zum schriftliche Dividieren

