Grundwert berechnen

Beispiel 1

Bei einem Einkauf bekommen wir 20% Rabatt und müssen noch 15€ bezahlen. Wie teuer wäre der Einkauf ohne Rabatt gewesen?

Wir notieren die gegebenen Größen. Dabei müssen wir darauf achten wie vielen Prozent den 15€ entsprechen. Wenn man die Aufgabe nicht genau liest, denkt man leicht, dass die 15€ 20% vom Grundwert darstellen. Jedoch ist es hier so, dass wir 20% Rabatt bekommen. Wir müssen also noch 80% vom ursprünglichen Preis bezahlen (100% – 20% = 80%). Die 15€ sind also 80% des Grundwerts. Wir notieren also:

Prozentsatz: 80% = 0,8
Prozentwert: 15€
Grundwert: ?

Wir setzen die Werte in die Formel ein und erhalten:

Ohne Rabatt hätten wir 18,75€ bezahlen müssen.

Alternativer Lösungsweg mit dem Dreisatz

Bei Prozentaufgaben handelt es sich um proportionale Zusammenhänge. 0% entsprechen auch immer einem Prozentwert von 0. Es gilt außerdem, dass wenn sich der Prozentsatz verdoppelt, sich auch der Prozentwert verdoppelt. Dadurch, dass es ein proportionaler Zusammenhang ist, können wir den Dreisatz anwenden.

Wir schreiben also wieder die Werte auf die wir kennen:

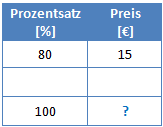
Wir kennen also den Preis der 80% entspricht und möchten wissen welcher Preis 100% entspricht. Um die 100% zu ermitteln gehen wir den Schritt über 1% und berechnen welcher Preis 1% entspricht indem wir beide Seiten durch 80 teilen. Anschließend müssen wir mit 100 multiplizieren um auf die gefragten 100% zu kommen.

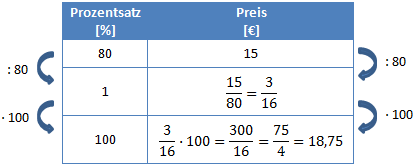
Auch hier kommen wir auf das Endergebnis, dass der ursprüngliche Preis 18,75€ entspricht. Welchen Weg man lieber geht ist Geschmackssache.