Herleitung / Beweis

Es gibt sehr viele Beweise für den Satz des Pythagoras. Er ist der meistbewiesene mathematische Satz. Wir möchten hier einen geometrischen Beweis zeigen.

Wir zeichnen in ein Quadrat vier gleiche rechtwinklige Dreiecke ein:

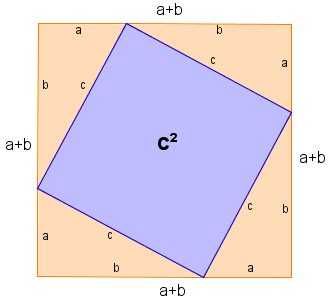
Dadurch bleibt in der Mitte ein Quadrat übrig, welches die Seitenlänge c hat. Der Flächeninhalt des inneren Quadrats ist damit c². Es gibt allerdings noch eine andere Möglichkeit 4 gleiche rechtwinklige Dreiecke in das Quadrat zu zeichnen:

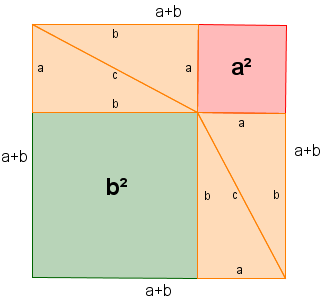
Bei diesem Quadrat behalten wir – nachdem wir die vier Dreiecke eingezeichnet haben – noch zwei Quadrate übrig. Eines hat den Flächeninhalt b², das anderen den Flächeninhalt a².
Da die beiden Ursprungsquadrate denselben Flächeninhalt (a+b)² haben und auch die vier Dreiecke in beiden Fällen denselben Flächeninhalt besitzen, muss auch der Rest der Fläche in beiden Fällen gleich groß sein. Es gilt also das c² genauso groß sein muss wie a² und b² zusammen. Daraus folgt:

Unser Lernvideo zu : Herleitung / Beweis