Höhe eines Dreiecks
Besonders um den Flächeninhalt eines Dreiecks bestimmen zu können, ist es wichtig die Höhe des Dreiecks zu kennen.
Unser Lernvideo zu : Höhe eines Dreiecks
Es gibt drei Höhenlinien, dies ist jeweils die kürzeste Strecke von einem Eckpunkt zur gegenüberliegenden Seite. Wenn man ein Lot (eine gerade Linie) von einem Eckpunkt auf die gegenüberliegende Seite fallen lässt, schneidet das Lot die Seite im sogenannten Lotfußpunkt.
Die Strecke zwischen Eckpunkt und Lotfußpunkt ist die Höhe, sie steht senkrecht (im rechtem Winkel) auf der Seite.
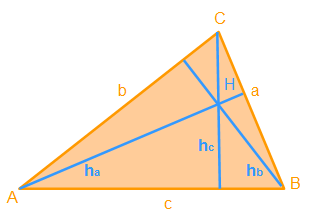
Die Höhe ha steht senkrecht auf der Seite a und verläuft durch den Eckpunkt A.
Die Höhe hb steht senkrecht auf der Seite b und verläuft durch den Eckpunkt B.
Die Höhe hc steht senkrecht auf der Seite c und verläuft durch den Eckpunkt C.
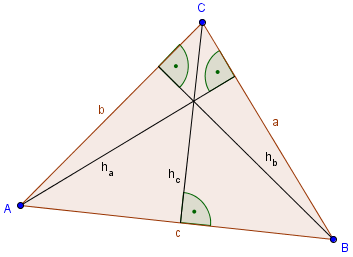
In der Abbildung sieht man die eingezeichneten Höhen ha, hb, und hc. Alle Strecken treffen sich in einem gemeinsamen Punkt, dem Höhenschnittpunkt. Dies ist bei jedem Dreieck der Fall.
Eine Höhe teil ein Dreieck in zwei rechtwinklige Dreiecke, dies kann man für viele Aufgaben nutzen.
Eine Höhenlinie und der Höhenschnittpunkt können auch außerhalb des Dreiecks liegen
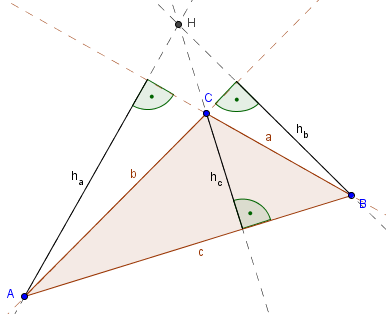
Bei diesem stumpfwinkligen Dreieck sehen wir, dass hc noch im Dreieck liegt. Die Höhenlinien ha und hb allerdings liegen außerhalb des Dreiecks. Die Seiten a und b sind gestrichelt weitergeführt, um zu demonstrieren, dass die Höhenlinien auch da senkrecht stehen.
Auch alle Höhenlinien sind gestrichelt weiter gezeichnet, da der Höhenschnittpunkt H auch außerhalb des Dreiecks liegt.
Höhen bei einem rechtwinkligen Dreieck
Bei einem rechtwinkligen Dreieck gibt es die Besonderheit, dass zwei der drei Höhen gleich zu den Seiten des Dreiecks sind.
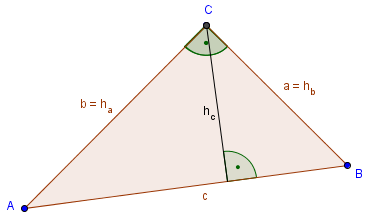
In der Abbildung sehen wir ein rechtwinkliges Dreieck, dass seinen rechten Winkel im Eckpunkt C hat.
Die Höhe hc liegt senkrecht auf der Seite c. Die Höhe ha ist die selbe Strecke wie die Seite b und die Höhe hb ist genau gleich zur Seite a. Auch diese beiden Höhen stehen, wie gelernt, senkrecht. Der Höhenschnittpunkt der drei Höhenlinien ist gleich dem Eckpunkt mit dem rechten Winkel, in diesem Beispiel dem Punkt C.
Bei rechtwinkligen Dreiecken ist es deshalb oft einfach die Höhe zu bestimmen. Mehr dazu erfährst du bei dem Satz des Pythagoras.
Konstruktion einer Höhe
Nun zeigen wir Schritt für Schritt, wie man eine Höhe mir Zirkel und Lineal zeichnet:
1. Schritt: Zuerst zeichnen und beschriften wir ein Dreieck dessen Höhen wir bestimmen wollen.
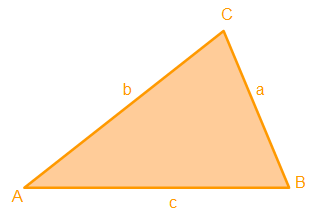
In unserem Beispiel sehen wir ein unregelmäßiges Dreieck. Alle Seiten und Eckpunkte sind beschriftet
2. Schritt: Nun legen wir als erstes fest, mit welcher Höhe wir beginnen wollen, z. B. mit der Höhe hc. Wir wissen, die Strecke läuft senktrecht vom Punkt C zur Seite c. Um dies richtig ermitteln zu können zeichnen wir zunächst einen Halbkreis mit dem Mittelpunkt im Eckpunkt C. Der Radius des Halbkreises muss die gegenüberliegende Seite c zweimal schneiden.
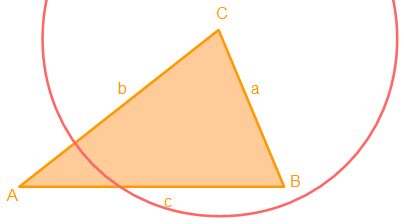
Der Halbkreis um den Punkt C schneidet die Seite c hier nur einmal, daher müssen wir die Seite c etwas nach rechts erweitern, so dass wir einen zweiten Schnittpunkt erhalten.
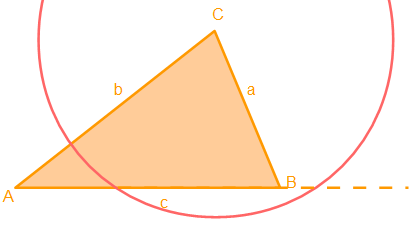
Die gestrichelte Hilfslinie verlängert die Seite c und wir erhalten einen zweiten Schnittpunkt mit dem Halbkreis.
3. Schritt: Als nächstes werden zwei Kreisbögen mit dem Zirkel gezeichnet. Die Mittelpunkte sind die eben ermittelteten Schnittpunkte der Seite c und des Kreises. Wichtig ist, dass man bei beiden Kreisbögen, den selben Radius nutzt! Er kann aber differenziert sein zum eben verwendeten.
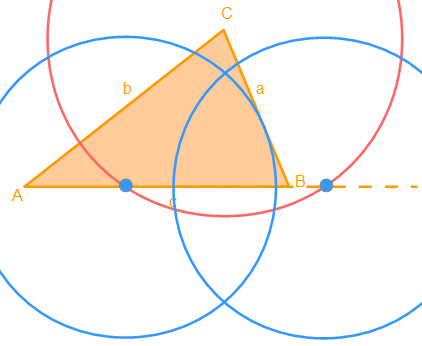
Die blauen Kreisbögen haben den selben Radius. Ihre Mittelpunkte (blaue Punkte) sind die Schnittpunkte des Hilfskreises mit der Seite C. Sie schneiden sich in zwei Punkten.
4. Schritt: Den roten Hilfskreis haben wir zur besseren Übersicht weggelassen, da wir ihn nicht mehr brauchen. Wir sehen, die Kreise schneiden sich in zwei Punkten. Wenn man nun eine Linie durch diese Schnittpunkte zeichnet, erhalten wir eine Gerade, die senkrecht zur Seite c und durch den Punkt C verläuft:
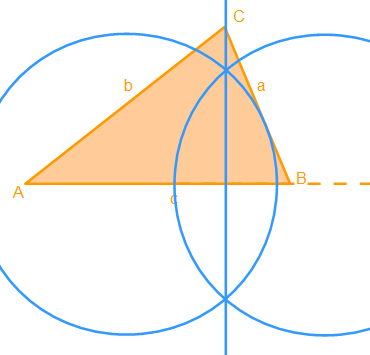
Die Gerade durch die Schnittpunkte der blauen Kreisbögen ist eingezeichnet. Wie erwartet ist sie senkrecht zur Seite c und läuft durch den Eckpunkt C.
5. Schritt: In diesem Schritt zeichnen wir nun die Höhe hc ein. Sie ist ein Teil der eben eingezeichneten Geraden und erstreckt sich von der Seite c zum Punkt C.
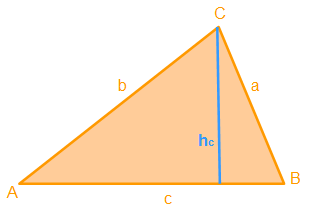
Alle Hilfslinien und Hilfskreise sind entfernt und wir haben die Höhe hc konstruiert.
Genauso werden alle Höhen konstruiert. Der Startpunkt ist jeweils der dazugehörige Eckpunkt der Höhe. Also beginnen wir bei der Höhe ha im Eckpunkt A und bei der Höhe hb im Eckpunkt B. Wenn nötig müssen die Seiten wie in unserem Beispiel verlängert werden.
Sind alle Höhen eingezeichnet, hat man auch den Höhenschnittpunkt ermittelt.