Integral aufleiten
Eine Funktion F heißt Stammfunktion einer Funktion f auf einem Intervall I, wenn für alle xI gilt:, F’(x) = f(x)
Man kann Stammfunktionen als „Mütter oder Väter der Funktion“ bezeichnen und die Ableitung von einer Funktion als „Kinder der Funktion“, sie sind also die „Enkel der Stammfunktionen“. Dieser Vergleich trifft die Situation im „Reich der Funktionen“ aber nicht ganz, denn eine Funktion hat höchstens eine Ableitung, aber unendlich viele Funktionen als Stammfunktionen.
→statt „aufleiten“ sagt man meist „integrieren
Man schreibt: ∫f(x) dx=F(x)+C
wobei C eine beliebige Konstante ist, da es zu jeder Funktion beliebig viele Stammfunktionen gibt, die sich nur in der Konstante unterscheiden (die fällt ja beim Ableiten wieder weg)
Merke
Zwischen Integral- und Stammfuntkion besteht folgender Zusammenhang: Jede Integralfunktion ist eine Stammfunktion, aber nicht umgekehrt. Alle Stammfunktion F zu f unterscheiden sich durch eine additive Konstante c. D. h. kennt man eine Stammfunktion, so kennt man alle.
Beispiel: Die Funktion F(x) = x2+ 1 ist eine Stammfunktion zu f(x) = 2x, da (x2+ 1)’ = 2x. Sie ist aber keine Integralfunktion zu f(x) = 2x, da gilt x 2 + 1 > 0 für alle x∈ und damit die Eigenschaft, dass jede Integralfunktion mindestens eine Nullstelle besitzt, nicht erfüllt.
Unterschied zwischen bestimmten und unbestimmten Integral
bestimmtes Integral: Das bestimmte Integral einer Funktion f(x) von a bis b
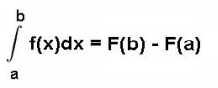
ist der Flächeninhalt der von der Funktionskurve und der x-Achse berandeten Fläche zwischen x = a und x = b. (Je nach Vorzeichen der Funktion und Integrationsrichtung trägt dieser Flächeninhalt ein positives oder negatives Vorzeichen)
Das unbestimmte Integral : Das unbestimmte Integral einer Funktion f(x) ist, ![]()
mit einer Stammfunktion F (x) von f (x), also: F′ (x) = f (x), und einer beliebigen Konstanten C, der sog. Integrationskonstanten

Beispiele
| f(x) | F(x) |
| 1 | x |
| 10 | 10x |
| x2 | 1/3x2 |
| 5x7 | 5/8x8 |
| 3x4-2x3+4 | 3/5x5-2/4x4+4x |
| 10x | 10x2 |
Merke: Beim Aufleiten muss der Exponent um 1 erhöht und in den Nenner des Bruchs geschrieben werden!
Die Umkehrung des Ableitens ist das Bilden von Stammfunktionen und wird deshalb auch Aufleiten genannt
