Fläche zwischen zwei Graphen
Wir haben bereits gelernt, wie man die Fläche zwischen dem Graphen einer Funktion und der x-Achse bestimmen kann. Mit diesem Wissen können wir ebenfalls die Fläche zwischen zwei Graphen berechnen.
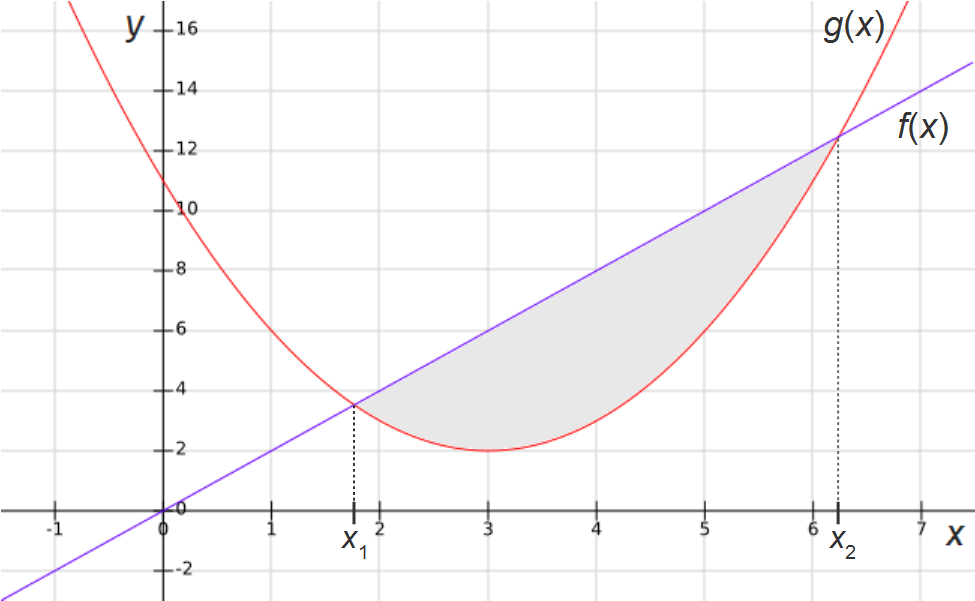
Zieht man das Integral der oberen Funktion f (x) von dem Integral der unteren Funktion g (x) ab, so erhält man die Differenz der Flächen, die von den Graphen der Funktionen und der x-Achse eingeschlossen werden. Diese Differenz entspricht der Fläche zwischen den Graphen der beiden Funktionen. Mathematisch ausgedrückt sieht das folgendermaßen aus:
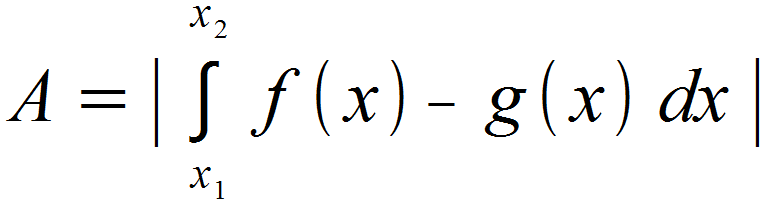
Die Integratiosgrenzen x1 und x2 stehen hier, wie auch in der Abbildung zu sehen, für die Schnittpunkte der beiden Graphen. Für den Fall, dass eine Fläche unterhalb der x-Achse bestimmt werden sollte, wird zusätzlich der Betrag des Integrals genommen, um negative Flächen zu vermeiden.
Unser Lernvideo zu : Fläche zwischen zwei Graphen
Beispiel
Wir suchen die Fläche, die von den Graphen folgender Funktionen eingeschlossen wird:
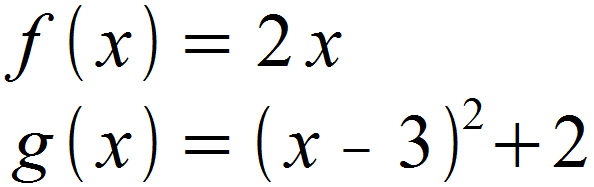
Die Graphen beider Funktionen sowie deren eingeschlossene Fläche sind auf der Beispielabbildung weiter oben zu sehen.
- Schnittpunkte bestimmen
Wir müssen zunächst die Intervallgrenzen herausfinden. Hierfür setzen wir die beiden Funktionen gleich, damit wir deren Schnittpunkte erhalten.
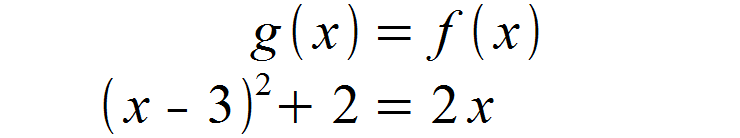
Wir lösen zunächst die Klammer nach der 2. binomischen Formel auf und ziehen 2 x auf die linke Seite.
![]()
Auf der linken Seite der Gleichung können wir dann zusammenfassen.
![]()
Nun haben wir die sogenannte „Normalform“ unserer quadratischen Gleichung vorliegen. Sie kennzeichnet sich vor allem dadurch, dass vor dem x2 kein Faktor steht und die rechte Seite der Gleichung gleich Null ist. Liegt die Normalform vor, können wir die p–q-Formel benutzen, dessen Variablen hier folgendermaßen definiert sind:
![]()
Die allgemeine p–q-Formel lautet wie folgt:
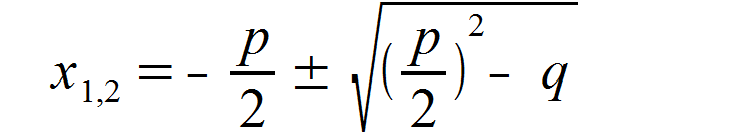
Um den ersten Schnittpunkt unserer Funktionen zu erhalten, setzen wir nun p und q in die Formel ein und wählen zunächst das negative Vorzeichen für die Wurzel.
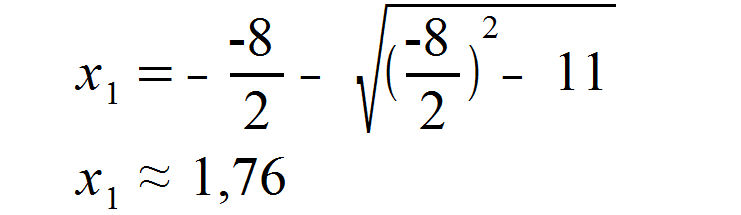
Die untere Intervallgrenze unseres Integrals haben wir nun bestimmt. Für den zweiten Schnittpunkt müssen wir lediglich das Vorzeichen der Wurzel ändern und erhalten:
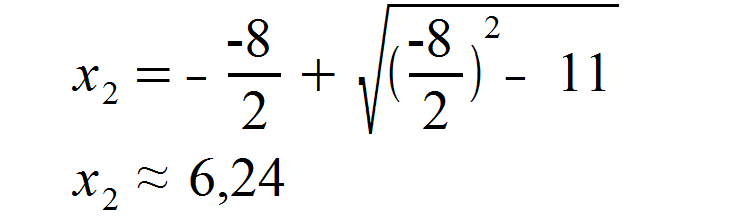
- Fläche zwischen den Graphen bestimmen
Uns liegen jetzt beide Intervallgrenzen vor. Diese setzen wir in die Formel für die Fläche ein.
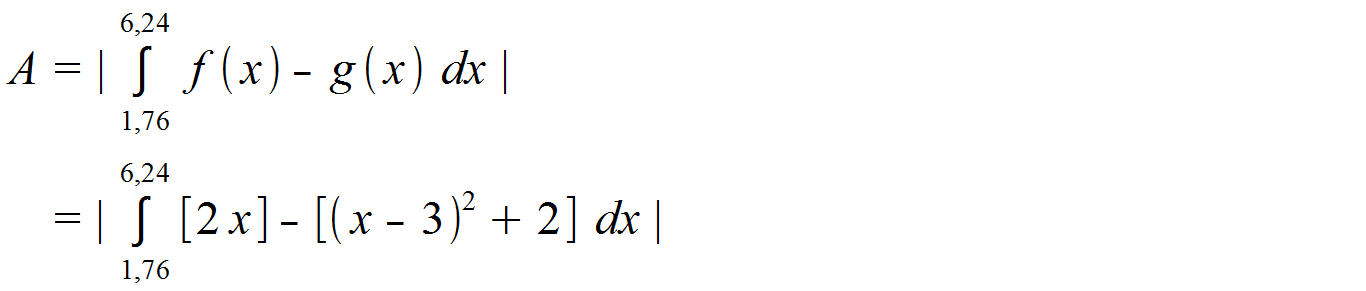
Die runde Klammer kann wieder nach den binomischen Formeln aufgelöst werden. Anschließend können wir die eckigen Klammern lösen. Durch das negative Vorzeichen vor der hinteren Klammer ist hierbei zu beachten, dass sich die Vorzeichen aller Terme in der Klammer umdrehen. Nach dem Auflösen können wir alle Terme zusammenfassen und erhalten:
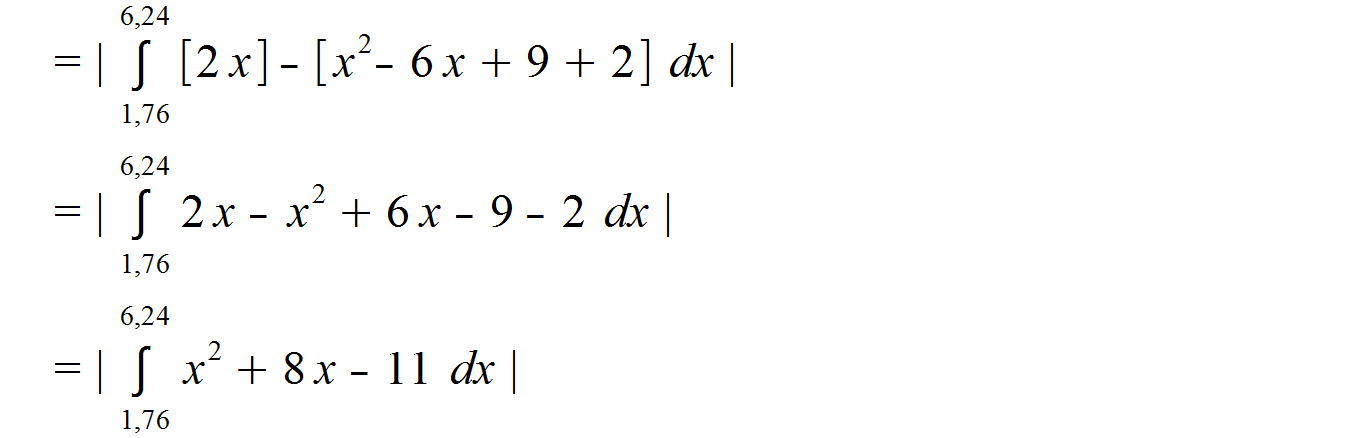
Anschließend integrieren wir die neue Funktion, die wir aus der Differenz von f (x) und g (x) bebildet haben. Es macht oftmals Sinn, wie hier erst die Funktionen voneinander abzuziehen und dann zu integrieren, um sich unnötige Arbeit zu sparen. Wir erhalten also:

Wir setzen daraufhin die Intervallgrenzen in die Stammfunktion ein und lösen somit das Integral.
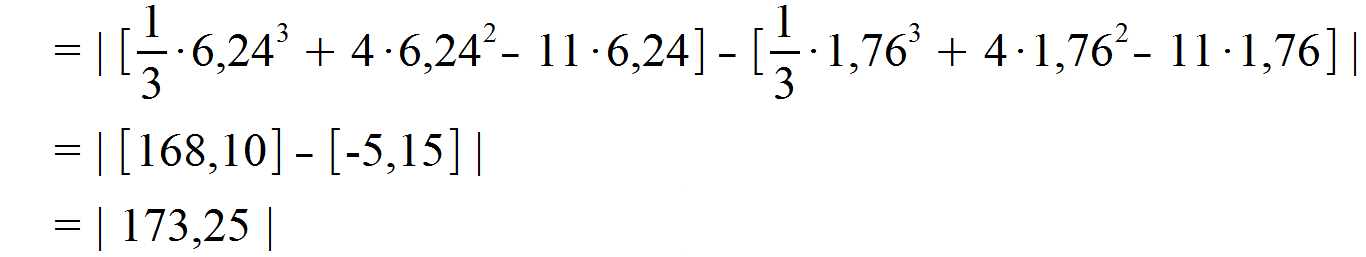
Abschließend nehmen wir noch den Betrag. Unser Ergebnis ist ohnehin schon positiv, weshalb dies nichts an dessen Vorzeichen ändert. Als Ergebnis unserer Fläche erhalten wir also folgenden Zahlenwert:
![]()
Kennt man die Einheit der Fläche nicht, fügt man üblicherweise noch FE an den Zahlenwert. FE steht für Flächeneinheit.
Beispiel mit wechselndem Vorzeichen
Nun soll die Fläche bestimmt werden, welche von den Graphen folgender Funktionen eingeschlossen wird:
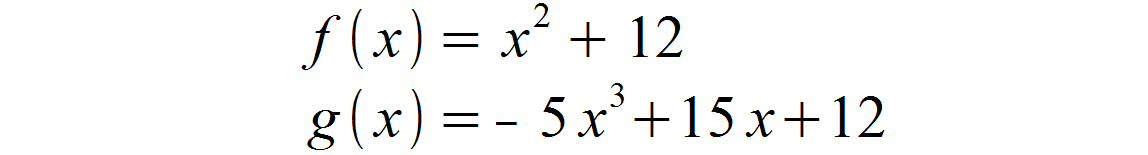
- Schnittpunkte bestimmen
Um die Intervallgrenzen herausfinden, müssen wir zunächst wieder beiden Funktionen gleichsetzen, damit wir deren Schnittpunkte erhalten.
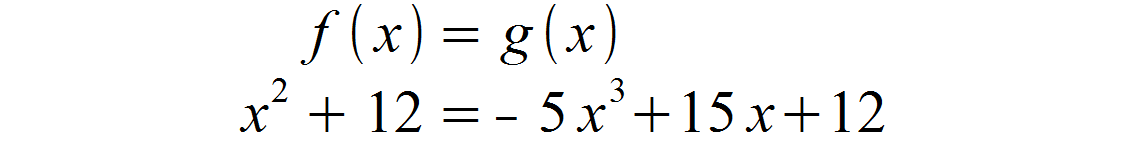
Anschließend formen wir die Gleichung nach Null um.
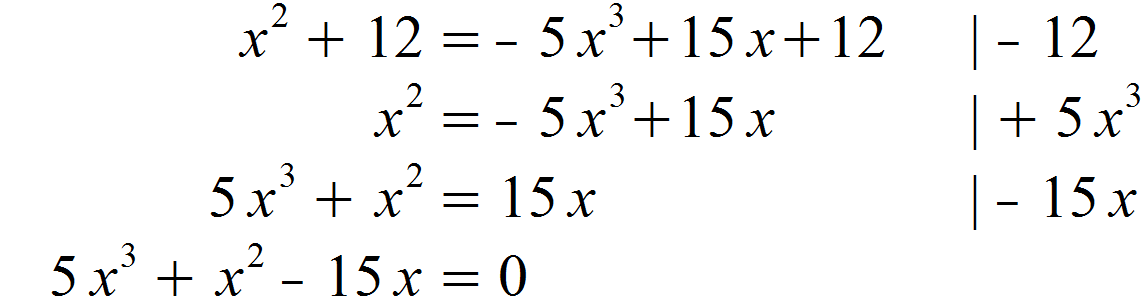
Da es sich bei x3 um die Potenz mit dem höchsten Exponenten handelt, liegt ein Polynom dritten Grades vor. In jedem Term befindet sich mindestens ein x, weshalb wir dieses ausklammern können.
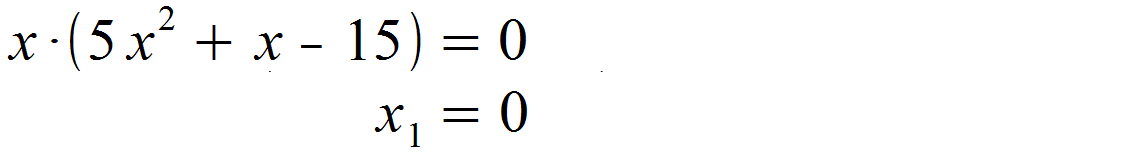
Diese Gleichung lässt sich mit x1 = 0 lösen und wir erhalten unseren ersten Schnittpunkt. Wenn der Inhalt der Klammer gleich Null ist, ergibt die linke Hälfte ebenfalls in jedem Fall Null. Deshalb stellen wir den Inhalt der Klammer frei und setzen ihn gleich Null.
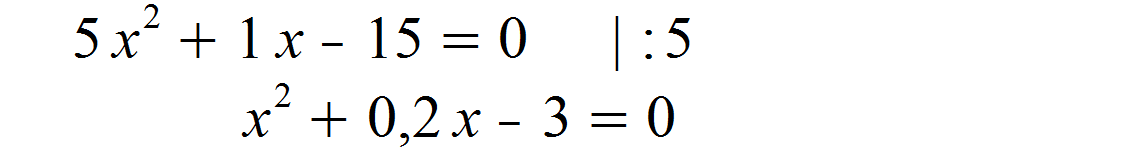
Um die p–q-Formel verwenden zu können, benötigen wir die Normalform. Das bedeutet hier, wir müssen x2 durch Umformung freistellen. Anschließend können wir der Gleichung sowohl p als auch q entnehmen.
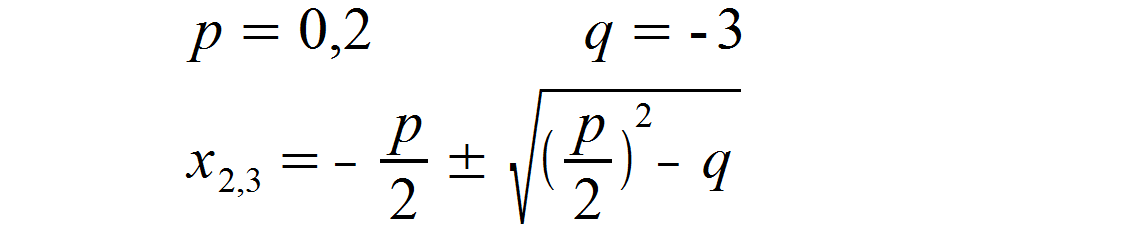
Der Index „2,3“ in der p–q-Formel steht dafür, dass sich durch Wählen des Vorzeichens vor der Wurzel zwei unterschiedliche x-Werte ergeben, die unterschiedlichen Variablen zuzuordnen sind. Da x1 schon vorliegt, werden hier also x2 und x3 berechnet. Wir wählen zunächst das negative Vorzeichen und setzen unsere Werte für p und q ein.
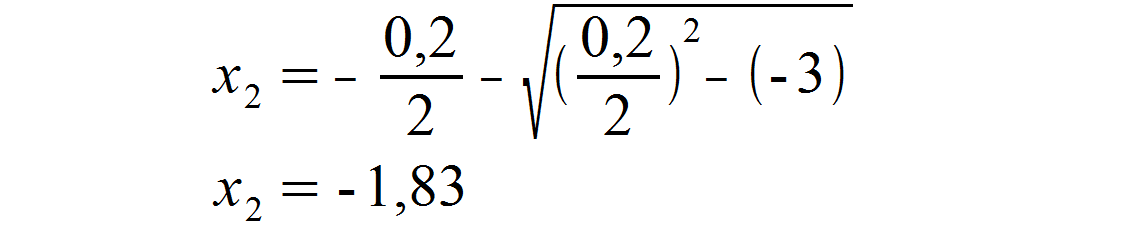
Anschließend wählen wir das positive Vorzeichen mit den gleichen p– und q-Werten und erhalten einen weiteren x-Wert.
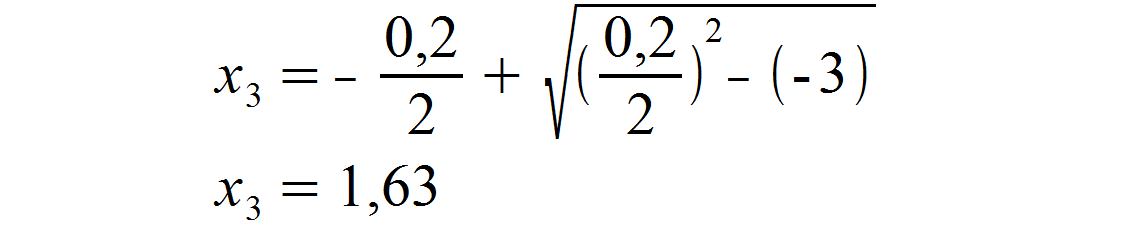
Wir haben also drei Schnittpunkte für die Graphen der untersuchten Funktionen erhalten. Wie müssen wir uns das nun vorstellen?
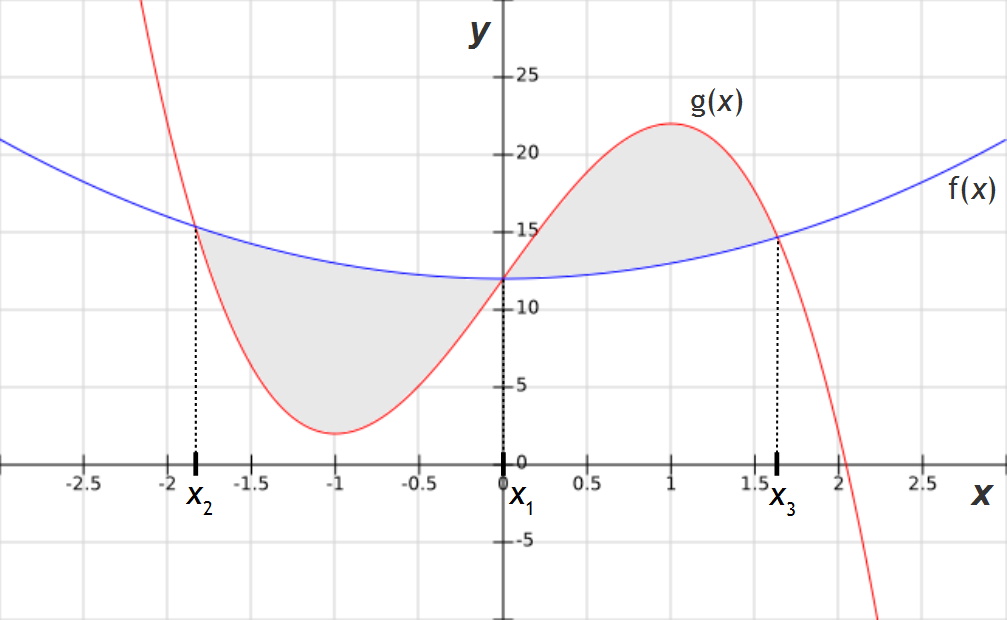
Auf der Darstellung sind beide Funktionen f (x) und g (x) sowie unsere drei x-Werte dargestellt. Für die Bestimmung der Fläche zwischen den Funktionsgraphen haben wir bisher die Differenz der Integrale beider Funktionen berechnet und einfach die zwei Schnittpunkte als Intervallgrenzen gewählt.
Nun liegen uns allerdings drei Schnittpunkte vor. Außerdem ergibt sich aus der Differenz f (x) – g (x) ab x = x2 zunächst ein positiver Wert, ab dem Schnittpunkt x1 wird diese Differenz jedoch negativ. Wählten wir also einfach das Integral von x2 bis x3, so erhielten wir ein verfälschtes Ergebnis, da die zweite Teilfläche von der ersten abgezogen würde.
- Fläche zwischen den Graphen bestimmen
Für die Berechnung müssen wir die Teilflächen also einzeln bestimmen und deren Beträge addieren, damit nur positive Flächen vorliegen. Wir bilden zunächst wieder das Integral der Differenz unserer Funktionen.
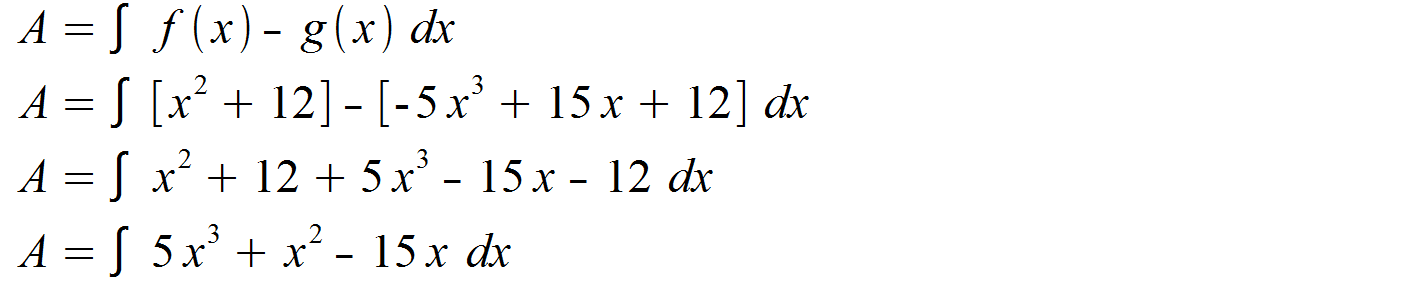
Wir setzen zunächst als Intervallgrenzen den unteren und mittleren x-Wert der Schnittpunkte ein. Anschließend lösen wir das Integral und erhalten die erste Teilfläche.
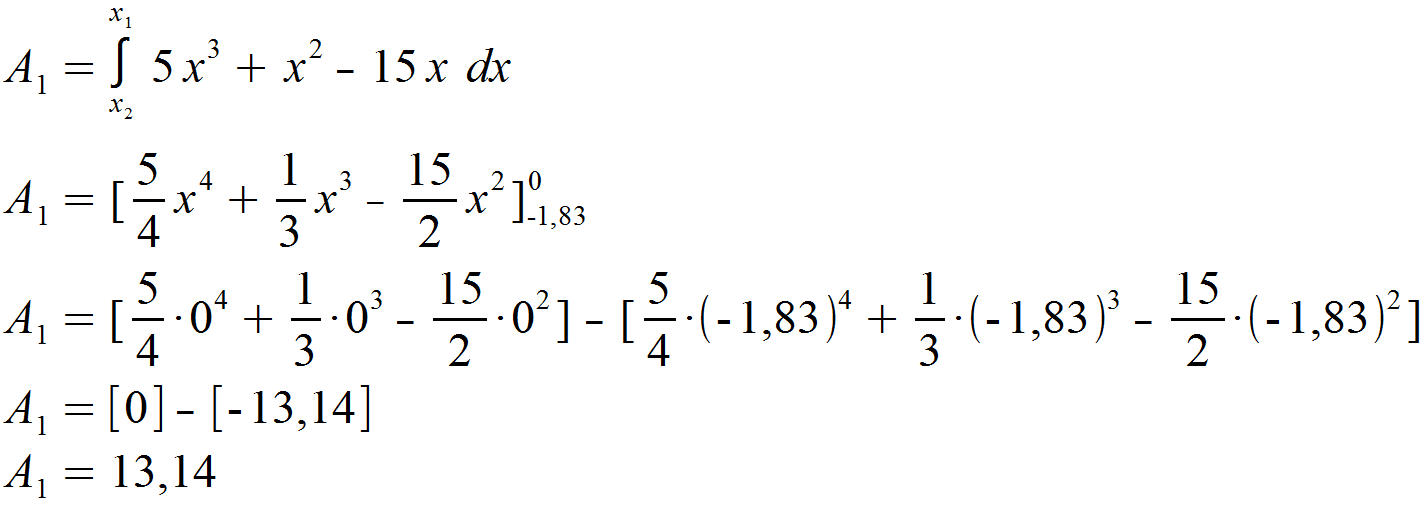
Den selben Weg gehen wir für den mittleren und oberen Schnittpunkte. Wie erwartet erhalten wir einen negativen Wert für unsere zweite Teilfläche, da die Funktion f (x) hier unterhalb von g (x) verläuft.
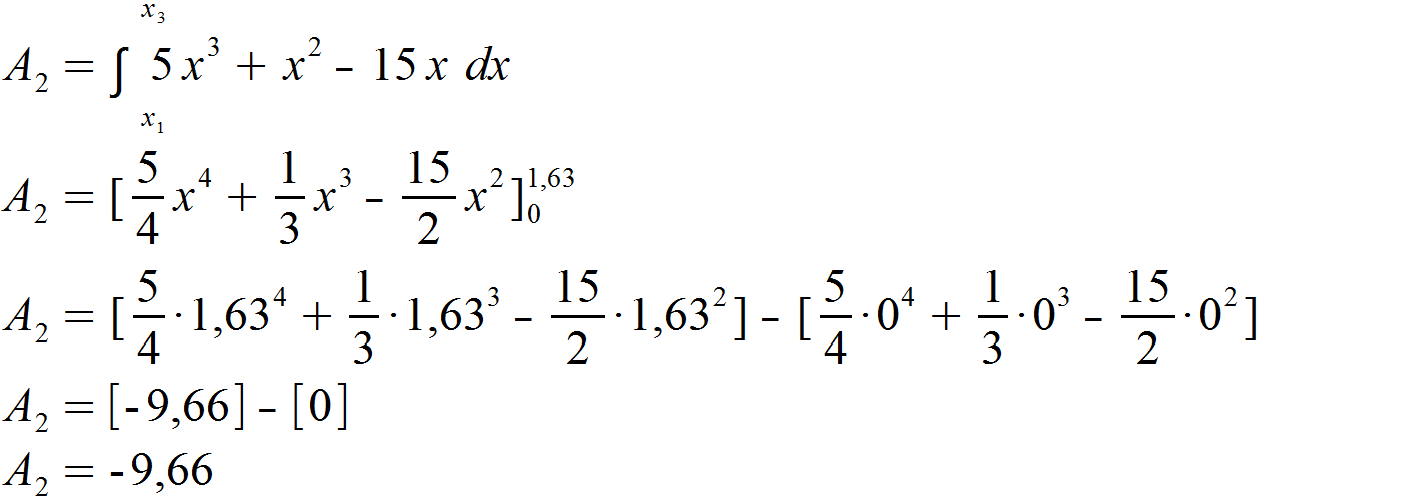
Nun addieren wir die Beträge unserer beiden Teilflächen, um negative Flächenanteile zu vermeiden.

Abschließend fügen wir wieder FE für Flächeneinheit an unseren Wert und erhalten somit eine Gesamtfläche von A = 22,80 FE.
