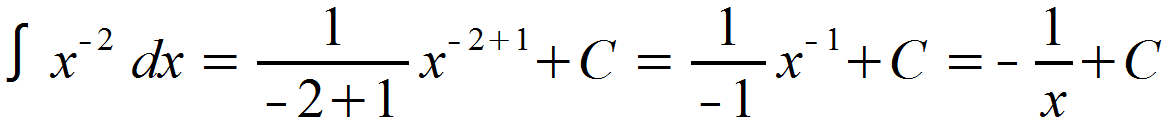Potenzregel bei Integration
Mit der Potenzregel kann man für alle Funktionen der Form f (x) = xn direkt die Aufleitung angeben. Der Exponent n ist hierbei eine beliebige rationale Zahl und x die Variable, nach der aufgeleitet wird.
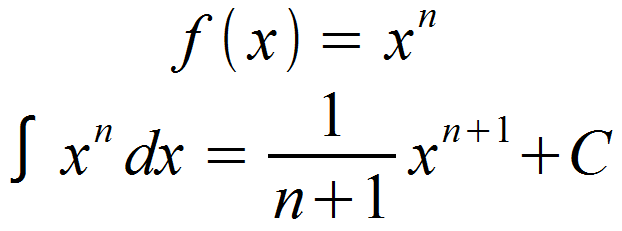
Zunächst gilt es also n zu identifizieren. Daraufhin addiert man 1 und erhält den neuen Exponenten n+1. Dieser neue Exponent bildet außerdem den Nenner im Bruch vor der Potenz.

Die oben genannte Regel kann für alle n ≠ -1 verwendet werden. Für den Fall n = -1 gilt:
![]()
Unser Lernvideo zu : Potenzregel bei Integration
Beispiel 1
Die nachfolgende Potentialfunktion soll nach dem Potenzgesetz aufgeleitet werden.
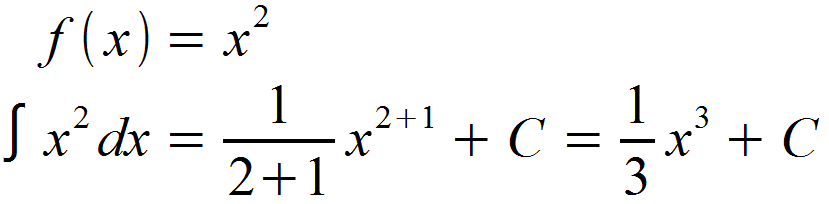
Wir erkennen n = 2 in f (x), addieren 1 und erhalten 3 als Exponenten der Potenz und Nenner für das Integral. Einmal verinnerlicht, ist die Potenzregel um Grunde ganz einfach. Hier noch ein paar Beispiele:
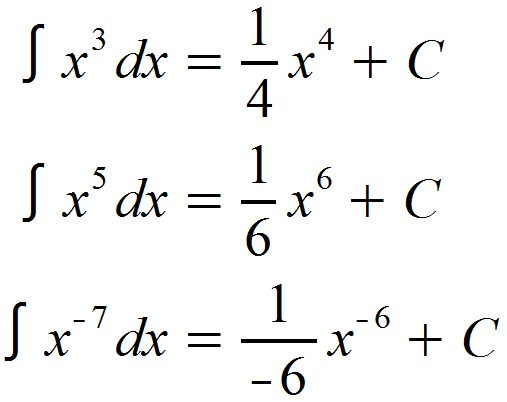
Diese Regel kann in vielen Fällen angewendet werden, in denen vielleicht nicht auf den ersten Blick eine Potenz erkennbar ist. So lassen sich auch Wurzeln und Brüche mit x im Nenner oftmals umschreiben und nach dem Potenzgesetz integrieren.
Beispiel 2
Bei Wurzeln wandert in der Potenzschreibweise der Grad der Wurzel in den Nenner des Exponenten. Das mag zunächst verwirrend klingen, ist jedoch recht einfach:
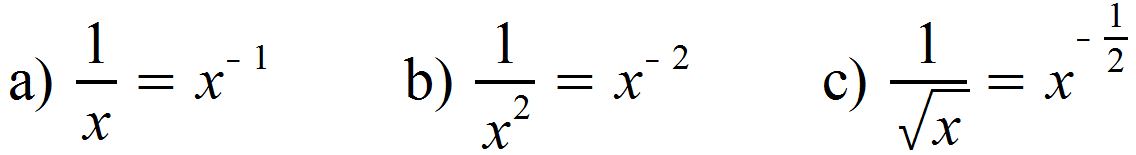
Falls all dies noch etwas verwirrend für dich klingt, findest du Erklärungen zu den Potenzregeln im Kapitel Exponentialrechnung. Einmal umgeformt können wir nun nach dem oben genannten Potenzgesetz integrieren. Wir behandeln den Exponenten n dabei wie jede andere Zahl.
Für Fall a) sieht das Integral dann folgendermaßen aus:
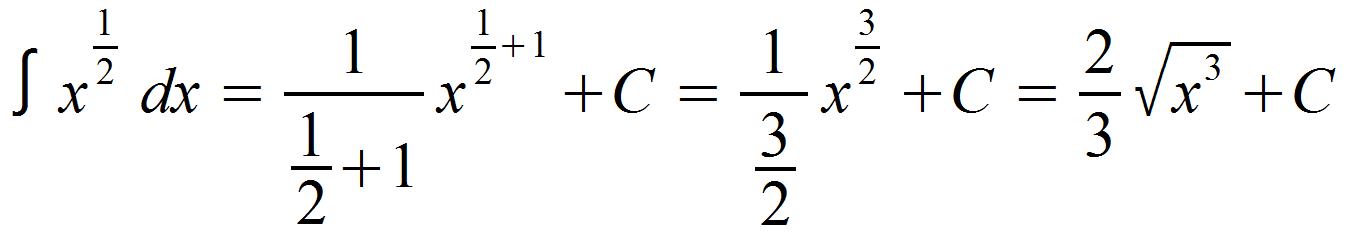
Beispiel 3
Bei Brüchen wird der Exponent von der Potenz im Nenner mit einem negativen Vorzeichen versehen. Auch hier klingt das komplizierter als es ist, hier also wieder ein paar Beispiele:
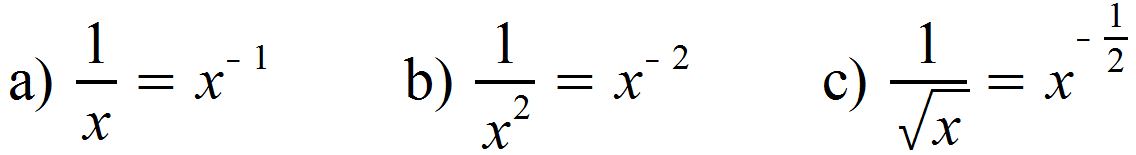
Für Fall a) können wir nicht regulär verfahren, sondern müssen nach dem Hinweis weiter oben integrieren und erhalten:
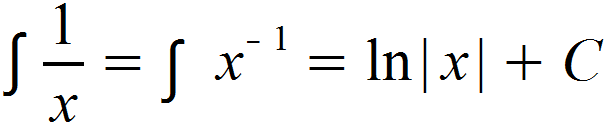
Integrieren wir also Fall b) ganz regulär nach der Potenzregel. Wir erhalten: