Substitution
Die Substitutionsregel (Substitution heißt Ersetzung) bei der Integration kann als Gegenstück zur Kettenregel beim Ableiten gesehen werden. Auch hier liegt wieder eine innere und eine äußere Funktion vor.
Die Regel scheint zunächst vielleicht komplizierter als die vorherigen, welche hier erklärt wurden, aber bei bestimmten Integranden (also Funktionen, die man integrieren will) bekommt man das Ergebnis mithilfe dieser Integrationsregel recht schnell und einfach.
Die Regel
Die Substitutionsregel ist hilfreich, wenn wir eine Funktion integrieren wollen, die wie das Ergebnis des Ableitens mit der Kettenregel aussieht. Wir suchen also eine Stammfunktion von f‚(z (t)) · z ‚(t). In Integralschreibweise sieht dies folgendermaßen aus:
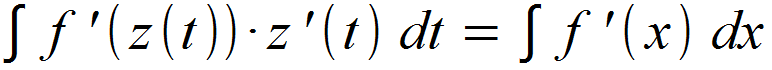
Wenn wir also die Funktion f ‚(z (t)) · z ‚(t) über t integrieren wollen, kann man dies als Integral der Funktion f ‚(x) über x auffassen. Das mag zunächst kompliziert klingen, ist in der Anwendung oftmals jedoch nicht allzu schwer und soll hier in einem Beispiel Schritt für Schritt verdeutlicht werden.
Unser Lernvideo zu : Substitution
Vorwissen
Die Ableitung z ‚(t) einer Funktion z (t) kann mathematisch auch folgendermaßen ausgedrückt werden.
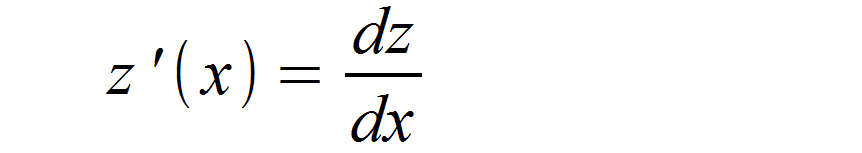
Das dx sollte dir noch aus der Integralschreibweise bekannt sein. Es steht hier allerdings im Nenner des Bruchs, was bedeutet, dass dz nach x abgeleitet wird und dies z ‚(x) ergbit. Für die Substitution stellen wir diese Gleichung nun nach dx um.
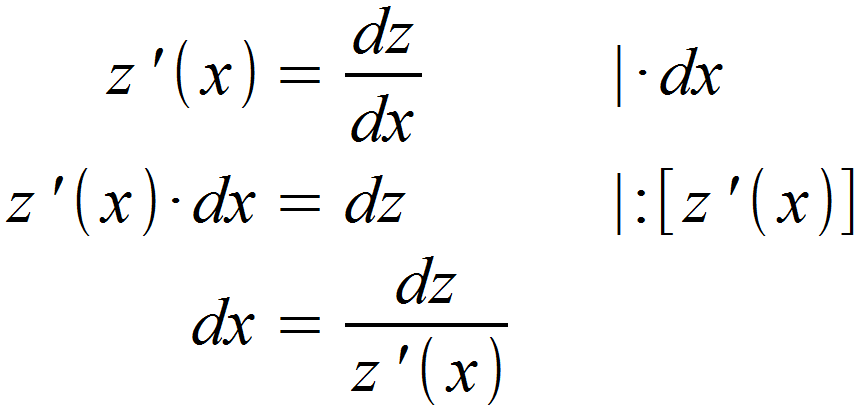
Nach dem ersten Schritt haben wir das dx in der uns bekannten Form und wissen somit, dass die Integration der Abeitung z ‚(x) nach x gleich dz ist. Teilen wir daraufhin durch die Ableitung z ‚(x), haben wir dx erfolgreich freigestellt.
Beispiel 1
Wir wollen die folgende Funktion integrieren.
![]()
Gleich im ersten Schritt führen wir die Substitution für die innere Funktion durch. Wir definieren also z = 5 x und setzen dies in das Integral ein.
![]()
Betrachten wir nun unsere Defintion von dx aus dem Vorwissen. Wir bilden hierfür die Ableitung von z (x) und erhalten z '(x) = 5, was wir in die Formel einsetzen.
Hinweis: Ob man als Schreibweise z oder z (x) verwendet, ist egal. Das (x) in z (x) ist lediglich ein Hinweis darauf, dass z von x abhängt.
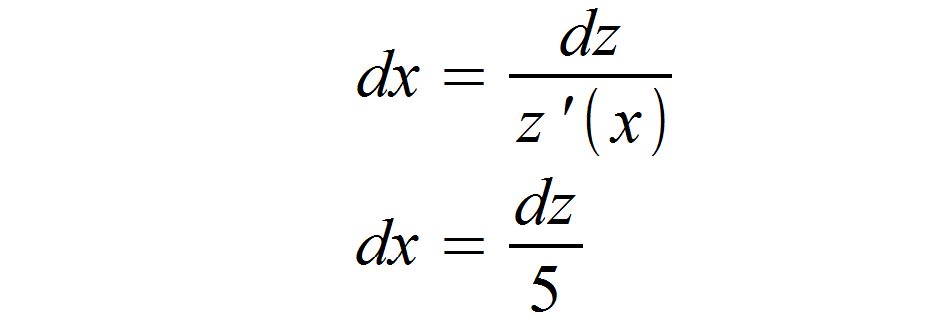
Dieses dx setzen wir nun in unser Integral mit der Substitution ein und erhalten:
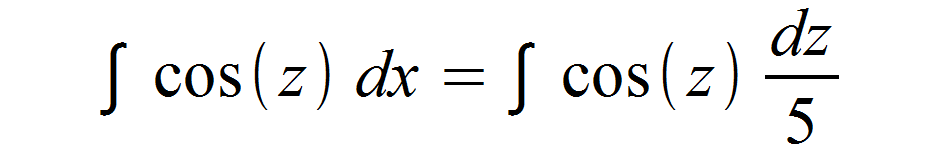
Wir können die 5 im Nenner aus dem Bruch holen und anschließend nach der Faktorregel aus dem Integral ziehen.
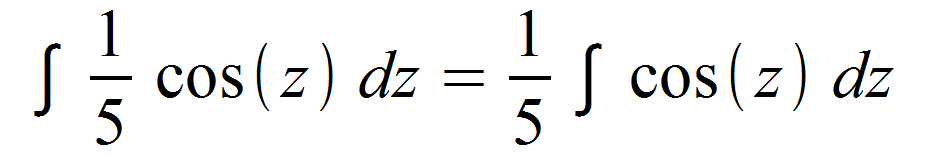
Anschließend kann wie gewohnt das Integral gelöst werden. Der einzige Unterschied hierbei ist nur, dass wir nach z und nicht wie sonst nach x integrieren müssen.
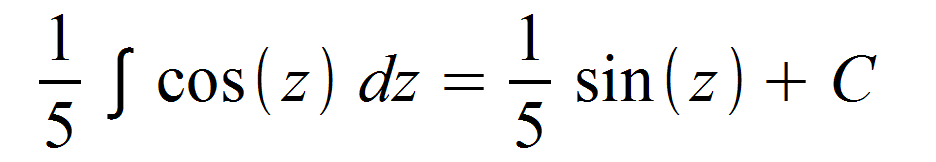
Im letzten Schritt rücksubstitutieren wir das z wieder und erhalten abschließend für unser Integral:
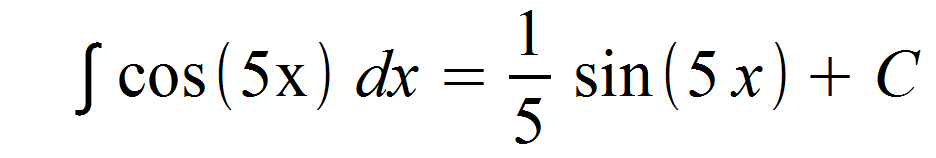
Beispiel 2
Die folgende Funktion ist zu integrieren:
![]()
Wir definieren zunächst wieder den zu substituierenden Term. Hier wählen wir den Exponenten der e-Funktion.
![]()
Im nächsten Schritt bilden wir die Integrationsvariable. Die Ableitung von z (x) = 9 x lautet z ‚(x) = 9.
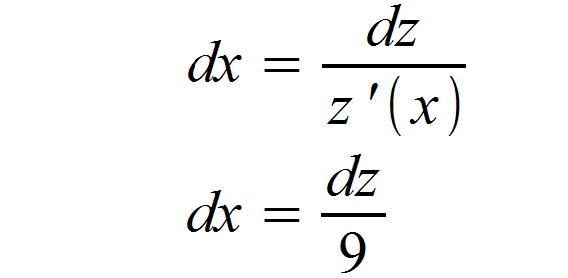
Als nächstes wird die Integrationsvariable in unser Integral eingesetzt.
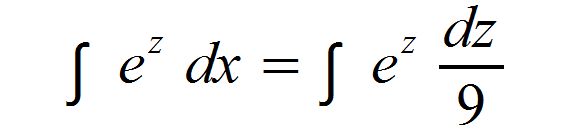
Wir können wieder den Nenner als konstanten Faktor herausziehen und integrieren daraufhin ez.
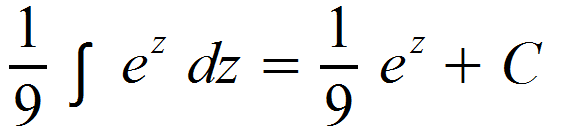
Somit erhalten wir als abschließende Lösung unseres Integrals:
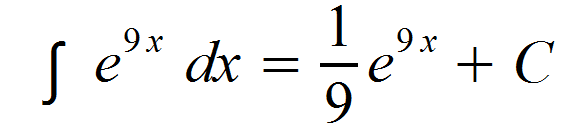
Die Arbeitsschritte lauten zusammengefasst:
- zu substituierenden Term als z definieren
- z (x) ableiten und damit Integrationsvariable dx bilden
- dx ersetzen
- Integral nach z lösen
- Rücksubstitution von z
