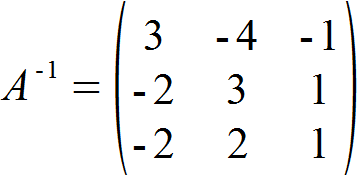Inverse einer Matrix

Die Inverse einer Matrix wird auch Kehrmatrix genannt und ist eine quadratische Matrix, die mit der Ausgangsmatrix multipliziert die Einheitsmatrix ergibt. Man kennzeichnet die Inverse mit einem hochgestellten „-1“, die Inverse einer Ausgangsmatrix A ist also A^-1.

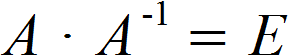
Matrizen, die eine Inverse besitzen, sind immer quadratisch. Das bedeutet, ihre Zeilenanzahl stimmt mit der Anzahl an Spalten überein. Ist eine Matrix invertierbar, so wird sie regulär genannt.

Es gibt verschiedene Verfahren, um die Inverse einer Matrix zu bestimmen. Hier soll die Berechnung anhand des sogenannten Gauß-Jordan-Algorithmus gezeigt werden.

Beispiel

Es soll die Inverse der regulären Matrix A gebildet werden.

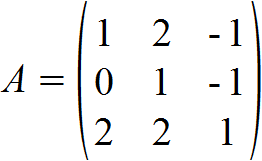
Wir wissen durch die oben genannte Bedingung, dass diese Matrix A multipliziert mit ihrer Inversen A^-1 die Einheitsmatrix ergeben muss. Mathematisch sieht das folgendermaßen aus:

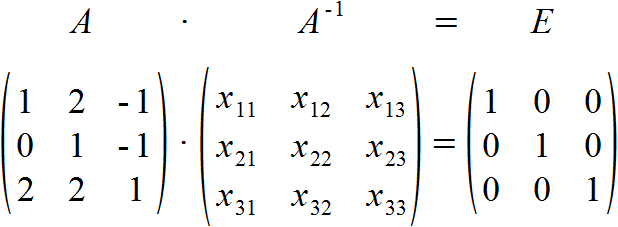
Gesucht sind also alle Elemente x_mn der Inversen A^-1, die diese Gleichung lösen. Wir nehmen hierfür die Ausgangsmatrix A sowie die Einheitsmatrix E und bilden aus ihnen die Blockmatrix (A|E).

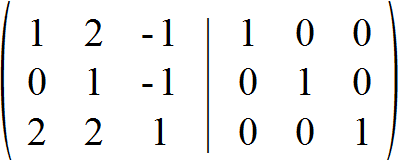
Nun müssen wir diese Blockmatrix soweit umformen, bis auf der linken Seite die Einheitsmatrix seht. Auf der rechten Seite befindet sich dann nämlich die gesuchte Inverse. Wir dürfen hierbei beliebig multiplizieren und dividieren sowie Zeilen addieren und subtrahieren.

Man geht zunächst am besten so vor, dass die linke Untermatrix in Dreiecksform gebracht wird. Dies bedeutet, dass alle Elemente unterhalb der Diagonalen gleich Null sein sollen. Dafür subtrahieren wir zunächst zweimal die erste Zeile von der dritten Zeile. Wir müssen diese Schritte immer für beide Seiten, also sowohl die Ausgangs- als auch die Einheitsmatrix durchführen.

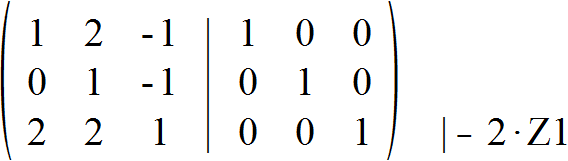
Nun haben wir bereits Null als erstes Element der dritten Zeile. Wir addieren die zweite Zweile im nächsten Schritt zweimal zur dritten Zeile.

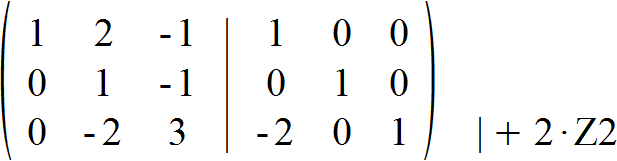
Nun beträgt das zweite Element der dritten Zeile ebenfalls Null und uns liegt die Dreiecksmatrix vor. Oftmals ist der Weg hierhin weitaus komplexer, ab diesem Schritt wird es allerdings in jedem Fall einfacher.

Wir wollen im weiteren Verlauf auch Nullen für die Elemente oberhalb der Diagonalen erhalten, weshalb wir zunächst die dritte Zeile zur zweiten Zeile addieren. Es empfiehlt sich nach Bildung der Dreiecksmatrix immer so vorzugehen, dass ein Vielfaches der letzten Zeile zur vorletzten Zeile addiert oder von ihr subtrahiert wird usw. Die Einheitsmatrix wird so Schritt für Schritt von unten aus gebildet und man spart sich unnötige Umformungen.

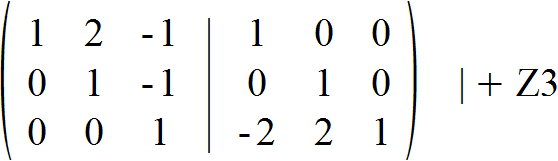
Nun entspricht sowohl die zweite als auch die dritte Zeile von der linken Untermatrix der gewünschten Einheitsmatrix. Im vorletzten Schritt addieren wir die dritte Zeile zur ersten Zeile.

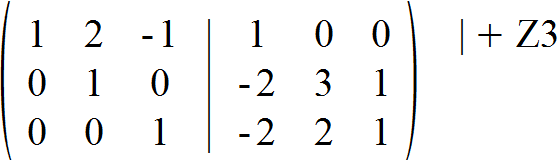
Wir haben unser Ziel fast erreicht. Im letzten Schritt subtrahieren wir noch die zweite Zeile zweimal von der ersten Zeile.

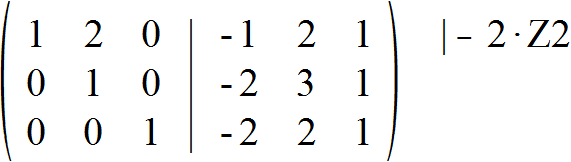
Uns liegt auf der linken Seite nun die Einheitsmatrix vor.

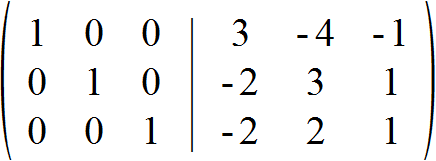
Die rechte Untermatrix entspricht der gesuchten Inversen A^-1, die wir abschließend also wie folgt angeben können: