Kantenschwerpunkt
In jedem Dreieck gibt es einen bestimmten Punkt, an dem man das Dreieck balancieren kann. Diesen Punkt nennt man Schwerpunkt. Genau an diesem Punkt ist das Gewicht komplett ausgeglichen.
Wir können unter drei verschiedenen Schwerpunkten unterscheiden:
– Flächenschwerpunkt: Die Masse ist gleichmäßig auf der Fläche verteilt.
– Eckenschwerpunkt: Die Masse sitzt in den Ecken und ist gleich verteilt.
– Kantenschwerpunkt: Die Masse ist gleichmäßig auf die Seiten verteilt.
Bei einem Dreieck stimmt der Flächenschwerpunkt und der Eckenschwerpunkt überein. Der Kantenschwerpunkt wird nur selten betrachtet, stimmt aber nicht mit den beiden anderen überein.
Unser Lernvideo zu : Kantenschwerpunkt
Kantenschwerpunkt ermitteln
Wir zeigen euch nun wie man den Kantenschwerpunkt eines Dreiecks ermittelt. Kurz gesagt ist es der Mittelpunkt des Innenkreises des Innendreiecks.
Wir betrachten ein allgemeines ebenes Dreieck ABC. Im ersten Schritt ermitteln wir die Mittelpunkte der drei Seiten. Also die Mitte von AB, von BC und von CA.
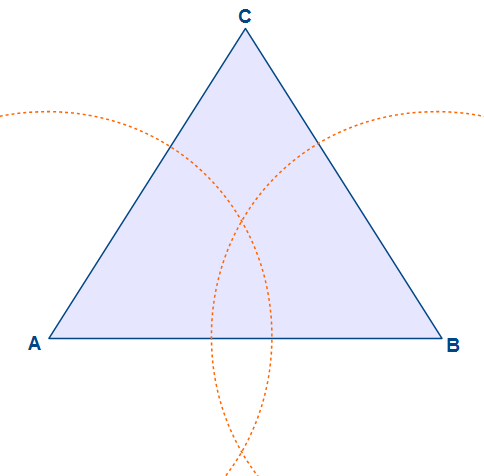
Um den Mittelpunkt einer Strecke mit dem Zirkel zu ermitteln, zeichnen wir je einen Kreis um die beiden Eckpunkte mit dem selben Radius. Die Kreise schneiden sich in zwei Punkte. Diese werden mit einander verbunden.
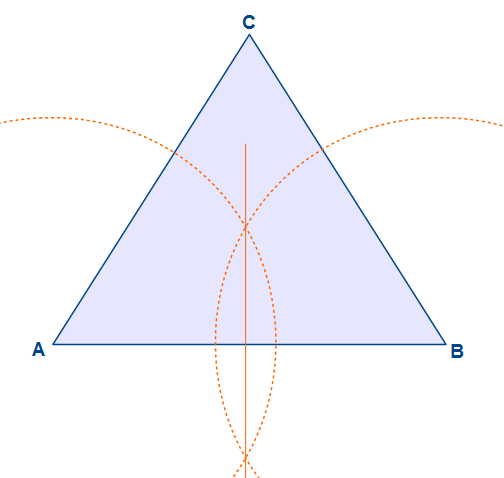
Die Verbindungslinie der beiden Schnittpunkte schneidet die Strecke AB genau im Mittelpunkt. Dieses zeichnen wir ein.
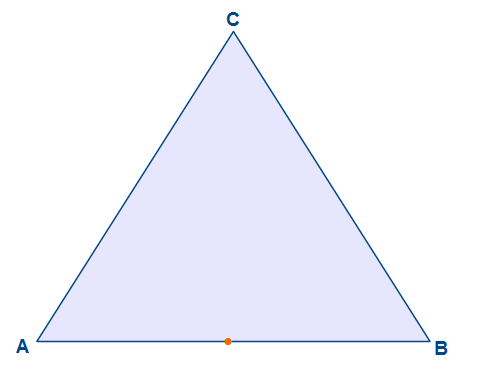
Nun haben wir den Mittelpunkt der Strecke AB eingezeichnet. Das selbe machen wir auch für die Strecken BC und CA.
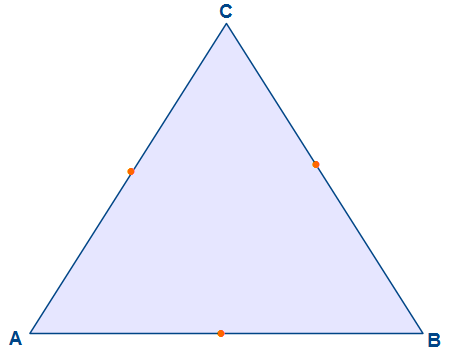
Nun haben wir alle Mittelpunkte ermittelt und verbinden diese.
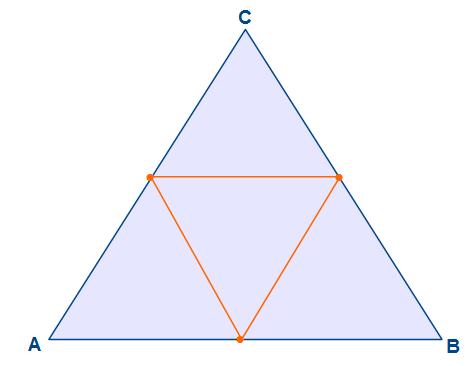
Nun haben wir das Innendreieck ermittelt und zeichnen als nächstes von jedem Winkel die Winkelhalbierende ein.
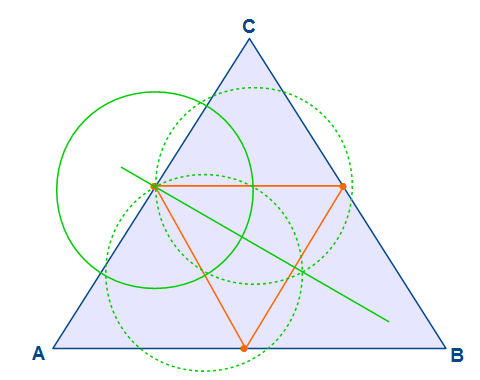
Um die Winkelhalbierende einzuzeichnen, ziehen wir zunächst einen Kreis um den Eckpunkt des Winkels. Dieser Kreis schneidet zwei Schenkel. Als nächstes ziehen wir um beide Schnittpunkte je einen Kreis mit dem selben Radius. Die beiden letzten Kreise schneiden sich einmal im Winkel und an einem weiteren Punkt. Diese Schnittpunkte werden verbunden, womit wir die Winkelhalbierende des Dreiecks eingezeichnet haben.
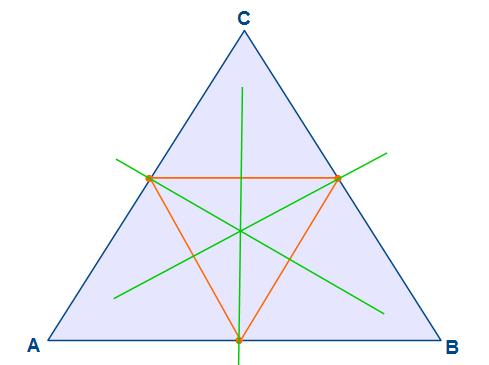
Wir zeichnen für jeden Winkel des Innendreiecks eine Winkelhalbierende. Alle treffen sich in einem Punkt. Dies ist zum einen der Mittelpunkt des Innenkreises als auch der Kantenscherpunkt des Dreiecks ABC.
Somit haben wir den Kantenschwerpunkt des Dreiecks ermittelt. Dieser Schwerpunkt kann mit den beiden anderen Schwerpunkten dem Eckenschwerpunkt und dem Flächenschwerpunkt zusammenfallen, aber dieses ist nur selten der Fall.
