Kettenaufgaben – Grundrechenarten üben
Kettenaufgaben sind sehr gut, um alle Grundrechenarten gemischt zu üben. Man sollte die einzelnen Grundrechenarten also schon relativ sicher beherrschen, bevor man sich an die Kettenaufgaben wagt. Wir gehen hier ein paar Beispiele durch.
Der Schwierigkeitsgrad ist dabei stark von den Aufgaben abhängig. Mit Punkt- vor Strichrechnung ist es natürlich deutlich schwerer als wenn man nur von links nach rechts rechnen muss. Besonders schwer sind die Aufgaben, wenn nicht die Lösung fehlt, sondern eine Zahl von der Rechnung.
1. Beispiel: Ohne Punkt- vor Strichrechnung
14 : 2 + 8 – 11 = ?
Wir gehen hierbei einfach von links nach rechts vor. Die Punkt- vor Strichrechnung beachten wir nicht, da sie durch die gegebene Reihenfolge der Rechnungen automatisch erfüllt wird.
Wir dividieren als Erstes 14 : 2 = 7. Dann addieren wir 7 + 8 = 15. Anschließend subtrahieren wir 15 – 11 = 4. Die Lösung ist also 8.
2. Beispiel: Mit Punkt- vor Strichrechnung
13 – 2 • 4 + 10 : 2 = ?
Bei diesem Beispiel rechnen wir ganz normal, also mit Punkt- vor Strichrechnung. Das genaue Vorgehen wurde im Kapitel „Rechenregeln“ bereits erklärt.
Wir multiplizieren zunächst 2 • 4 = 8 und dividieren 10 : 2 = 5. Nach Abschließen aller Punktrechnungen können wir die erhaltenen Ergebnisse in die Rechnung einsetzen und erhalten 13 – 8 + 5 = 10. Das Endergebnis ist also 10.
3. Beispiel: Eine Zahl der Rechnung fehlt
8 + 2 • ? : 3 – 2 = 10
Am schwierigsten ist es dann, wenn eine Zahl in der Gleichung fehlt. Dann müssen wir rückwärts rechnen und die Gleichung so lösen.
Wir müssen versuchen das Fragezeichen zu isolieren. Deshalb rechnen wir zunächst die bekannten Teile aus. Dies ist hier 8 – 2 = 6. Wir können also folgende vereinfachte Gleichung aufschreiben:
6 + 2 • ? : 3 = 10
Das Ergebnis von 2 • ? : 3 muss 4 sein, damit die Gleichung stimmt (6 + 4 = 10). Wir haben also die Gleichung:
2 • ? : 3 = 4
Jetzt kann man (zum Beispiel durch ausprobieren) relativ einfach auf die 6 kommen. 2 • 6 : 3 = 4, also ist die Lösung hier 6.
Alternatives systematisches Vorgehen
Wir stellen die Gleichung nach dem Fragezeichen um. Wir ziehen also alle anderen Teile nach rechts:
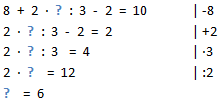
Dieses Vorgehen erfordert jedoch deutlich größeres mathematisches Verständnis und ist vermutlich nicht für die Grundschule geeignet.
