Kettenregel bei Ableitungen
Die Kettenregel hat ihren Namen daher, dass sie angewendet wird, um zwei oder mehrere miteinander verketteten Funktionen abzuleiten. Die Kettenregel ist aber gleichzeitig eine der wichtigsten und vielseitigsten Regeln der Differentialrechnung.
Entscheidend bei der Anwendung von Kettenregel, dass es sich bei der Ausgangsfunktion um eine verkettete Funktion handelt. Ganz allgemein handelt es sich meistens um eine verkettete Funktion, wenn sich eine oder mehrere der folgenden Funktionen im Term befinden:
- Exponenten um Klammern
- e-Funktionen
- Betragsfunktionen
- Wurzeln
- Trigonometrische Funktionen
- Logarithmen
Die Anwendung der Kettenregel
Die Anwendung findet man am häufigsten (als Teil) in einer Kurvendiskussion, wenn zum Beispiel Extrema oder Wendepukte einer Funktion berechnet werden. Oft findet man das Teil auch in der zweiten Ableitung einer gebrochenrationalen Funktion. Die Kettenregel ist ein wichtiger Bestandteil der Kurvendiskussion .
Vorgehensweise:
- u (x) und v (x) bestimmen
- u ‚(x) und v ‚(x) bilden
- in die Formel einsetzen
- ggf. ausmultiplizieren und vereinfachen
Die Kettenregel wird benutzt, wenn in einer Klammer ein x steht und gleichzeitig die Klammer außerhalb eine Hochzahl hat. Zudem wird die Kettenregel bei e-Funktion, sinus-, cosinus-Funktionen verwendet.Bei der Kettenregel wird die äußere Funktion zuerst abgeleitet und vor die gesamte Ableitungsfunktion geschrieben. Danach wird die innere Funktion abgeleitet und mit der äußeren Ableitung multipliziert.
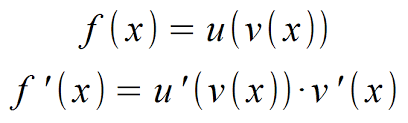
►Bei der äußeren Ableitung wird das betrachtet, was außerhalb der Klammer bei f(x) steht
►Bei der inneren Ableitung, wird das betrachtet, was innerhalb der Klammer bei f(x) steht
►Danach wird die innere Ableitung mit der äußeren Ableitung multipliziert
Beispiele
f(x)= cos(x2)
Äußere Funktion: cos(x)
Innere Funktion: x2
Ableitung äußere Funktion : -sin(x2)
Ableitung innere Funktion : 2x
Zusammengefasst: -sin(x2) * 2x
Beispiel
f(x)= -cos(4x)
Äußere Funktion: -cos
Innere Funktion: 4x
Ableitung äußere Funktion : sin
Ableitung innere Funktion : 4
Zusammengefasst: 4*sin(4x)
