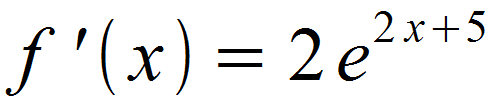Kettenregel zum Ableiten
Besteht die zu untersuchende Funktion aus mehreren zusammengesetzten, ineinander verschachtelten Funktionen, ist bei der Ableitung die Kettenregel anzuwenden.
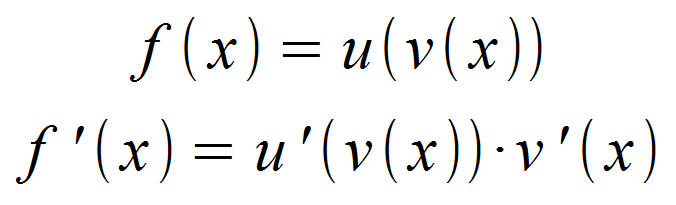
Man geht folgendermaßen vor:
- u (x) und v (x) identifizieren
- u ‚(x) und v ‚(x) bilden
- in die Formel einsetzen
- ggf. ausmultiplizieren und vereinfachen
Beispiel 1
Die folgende Sinusfunktion soll abgeleitet werden.
![]()
Wir identifizieren zunächst u (x) und v (x), wobei bei der Definition von u (x) die innere Funktion mit v substituiert wird.
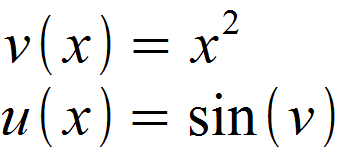
Als nächstes bilden wir u (x) und v (x). Für u (x) leiten wir hierbei nach v ab.
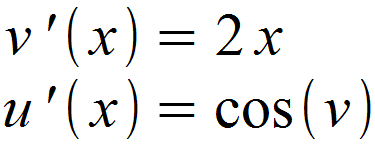
Die erhaltenen Ableitungsfunktionen setzten wir nun in die Formel ein.
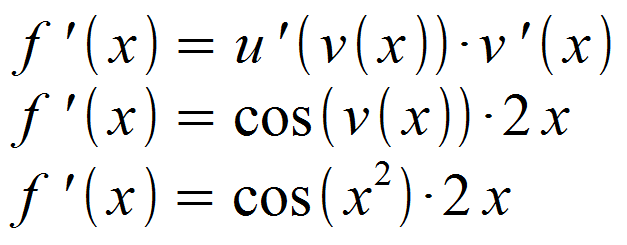
Im letzten Schritt ist gegebenenfalls auszumultiplizieren und zu vereinfachen. Hier lässt sich jedoch nicht weiter verfahren, also erhalten wir abschließend:
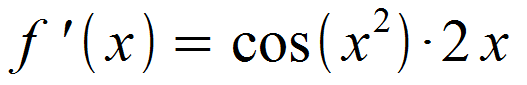
Unser Lernvideo zu : Kettenregel zum Ableiten
Beispiel 2
Die nachfolgende Funktion soll mithilfe der Kettenregel abgeleitet werden.
![]()
Zunächst identifizieren wir wieder u (x) und v (x), wobei die innere Funktion von u (x) erneut mit v substituiert wird.
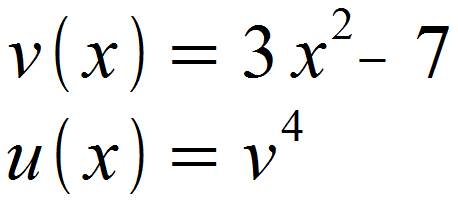
Als nächstes bilden wir u '(x) und v '(x).
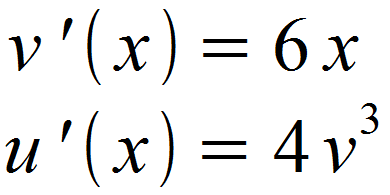
Die erhaltenen Funktionen setzen wir daraufhin in die Formel für die Ableitung ein.
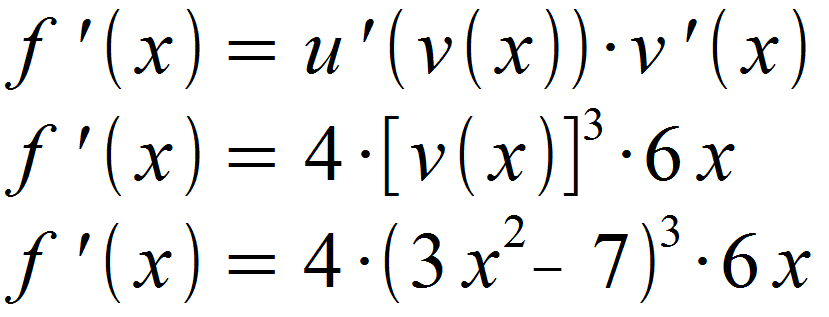
Durch abschließendes Ausmultiplizieren und Vereinfachen erhalten wir:
![]()
Beispiel 3
Die folgende Exponentialfunktion soll mithilfe der Kettenregel abgeleitet werden.
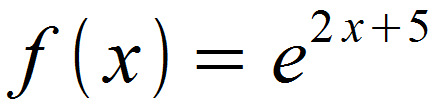
Wir identifizieren u (x) und v (x) und substituieren die innere Funktion von u (x) mit v.
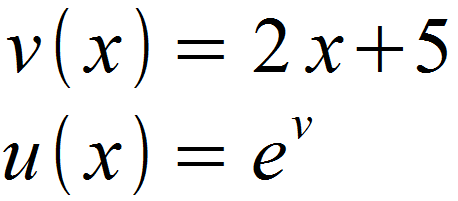
Anschließend wird u ‚(x) und v ‚(x) gebildet.
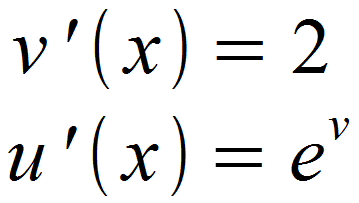
Die erhaltenen Funktionen werden wieder in die Formel für die Ableitung eingesetzt.
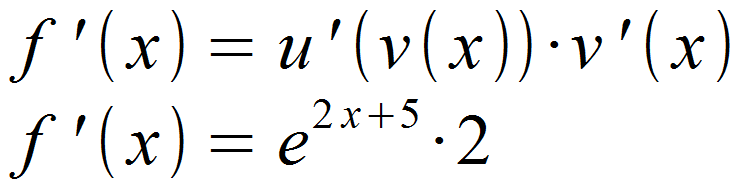
Das abschließende Ausmultiplizieren und Vereinfachen entfällt hier. Somit lautet die Ableitung von f (x):