Kollinearität eines Vektors
In der linearen Algebra bedeutet Kollinearität bei Vektoren eines Vektorraums, dass der von diesen Vektoren aufgespannte Untervektorraum die Dimension1 hat. Falls nur zwei vom Nullvektor verschiedene Vektoren betrachtet werden, ist Kollinearität gleichbedeutend damit, dass – vereinfacht gesprochen – jeder der beiden Vektoren durch Multiplikation mit einem Skalar, in den jeweils anderen Vektor überführt werden kann und beide linear abhängig sind
Kollineare und Komplanare Vektoren
Zwei Vektoren, deren Pfeile parallel verlaufen bezeichnet man als kollinear. Das bedeutet, dass sich ein Vektor als Vielfaches des anderen Vektors darstellen lässt.
Drei Vektoren, deren Pfeile sich in ein und derselben Ebene darstellen lassen bezeichnet mal als komplanar.
Unser Lernvideo zu : Kollinearität eines Vektors
Kollinearität
Parallele Vektoren haben die gleiche Steigung m = tan α.
Man nennt solche Vektoren kollinear oder linear abhängig.
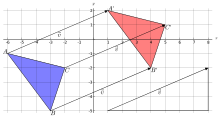
Beispiel
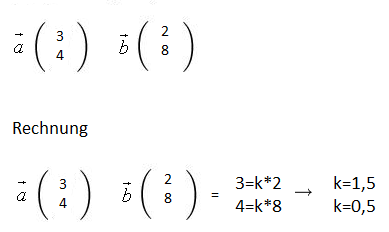
Die beiden Vektoren sind nicht kollinear (linear unabhängig) !
Beispiel 2
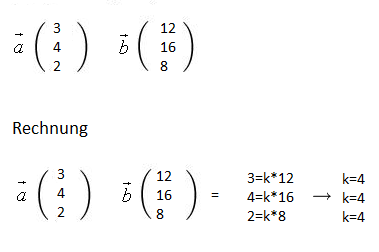
⇒gleichzeitig erfüllbar
Die beiden Vektoren sind kollinear (linear abhängig) !
Beachte
♦Drei linear abhängige Vektoren können untereinander parallel sein (paarweise linear abhängig) (mit 2 oder 3 Vektoren). Oder sie liegen wegen des geschlossenen Vektordreiecks in einer gemeinsamen Ebene: Komplanarität.
♦Genau dann, wenn die Vektoren linear abhängig sind, lässt sich einer von ihnen (mit Koeffizienten ≠ 0) durch eine Linearkombination der restlichen Vektoren ausdrücken.
