Koordinatengleichung zu Parametergleichung
Parametergleichung
Die Ebene wird eindeutig durch 3 kolineare Punkte P1,P2,P3 definiert
Die Parametergleichung besteht aus einem Festpunkt und zwei Richtungsvektoren ,welche die Ebene aufspannen. Der Festpunkt ist der Ortsvektor von P1 . Die Richtungsvektoren erhält man, indem man die Differenz zwischen den anderen Ortsvektoren bildet
Koordinatengleichung
Die Koordinatenform ggf Koordunatengleichung ist letztlich nichts anderes als die ausmultiplizierte Version der Normalenform einer Ebene. Daher ist sie auch auf die selbe Weise aufgebaut: In der Gleichung kommt der Normalenvektor der Ebene vor, sowie ein Punkt der in der Ebene liegt. Das reicht aus, um die Ebenengleichung zu bilden. Die Koordinatenform hat den Vorteil, dass man mit ihr innerhalb kürzester Zeit ausrechnen kann, ob ein bestimmter Punkt in der Ebene liegt.
Bei der Darstellung zeigt der Stützvektor auf einen bestimmten Punkt im Raum. Von dort aus geht der Richtungsvektor ab. Dieser kann durch die Variable (lambda oder andere Buchstaben) beliebig in seiner Länge verändert werden. Dadurch kann jeder Punkt auf der Geraden bestimmt werden. Man hat also in gewisser Weise ein Koordinatensystem im Raum, bei dem der Stützvektor auf den Ursprung zeigt und von dem der Richtungsvektor abgeht – als einzige Achse des Koordinatensystems.
Das einzige was sich bei der Ebenendarstellung ändert ist, dass sozusagen eine zweite Achse dazukommt. Ist ja auch logisch, denn eine Ebene ist ja eine Fläche, nicht eine Gerade und um eine Fläche zu bestimmen, braucht man nunmal zwei Achsen. Zeichnet man ein zweidimensionales Koordinatensystem auf ein Blatt Papier, dann kann man jeden Punkt auf diesem Blatt bestimmen – man muss nur die entsprechenden x und y-Werte haben.
Vorgehensweise
- Koordinatenform nach x2 auflösen
- x1 durch λ ersetzen
- Parameterform aufstellen
Beispiel
2x + 3y + 4z = -5
Wir setzen direkt x auf r und y auf s und stellen die Koordinatengleichung nach z um:
x = r
y = s
2r + 3s + 4z = -5
4z = -5 – 2r – 3s
z = -1,25 – 0,5r – 0,75s
Das ganze können wir auch so aufschreiben
x = 0 + 1r + 0s
y = 0 +0r +1s
z = -1,25 + (-0,5)r +( -0,75)s
in Vektorschreibweise sieht es dann so aus
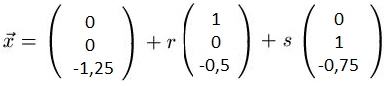
Fertig!
►Wir haben das ganze mit der Methode „direkte Parametisierung“ gelöst. Es gibt noch die Methode „Drei Punkte Gleichung) , wobei die erste Methode die einfachste ist!
♦Der einfachste Weg, um von der Koordinaten- zur Parameterform zu kommen ist es, sich einfach über die Koordinatenform drei Punkte in der Ebene zu suchen. Dazu muss man lediglich beliebige Punkte einsetzen und prüfen, ob das Ergebnis wahr ist (dann liegt der Punkt in der Ebene).
Hat man die drei Punkte, dann daraus einfach eine Ebene in Parameterform bilden: Ortsvektor zu einem der drei Punkte als Stützvektor und zwei linear unabhängige Vektoren bilden, die dann als Richtungsvektoren verwendet werden.
