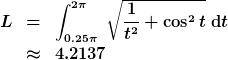Kurvenlänge durch Integration
Zwei verschiedene Wege können dasselbe Bild haben, dieselbe Kurve kann also durch verschiedene Wege parametrisiert werden. Es ist naheliegend, die Länge einer Kurve als die Länge eines dazugehörigen Weges zu definieren; das setzt aber voraus, dass die Länge für jede Parametrisierung denselben Wert liefert
Definitionen
Was ist eine Kurvenintegration
- Kurvenintegral: das ist der kürzeste weg zwischen zwei punkten ( also egal wie das inegral verläuft, ich nehme den kürzesten weg, wie zb. bei der potential im elektrischen feld)?
Was ist eine Integration?
- Das Integral ist ein Oberbegriff für das unbestimmte und das bestimmte Integral. Die Berechnung von Integralen heißt Integration. Erinnert euch an Flächen und Volumenberechnung
Wie kann man die Länge definieren?
- Die Länge ist in der Mathematik eine Eigenschaft, die Strecken,Wegen und Kurven zugeordnet werden kann. Die Länge einer Kurve wird auch als Bogenlänge bezeichnet
Formel für Kurvenintegration
![]()
Unser Lernvideo zu : Kurvenlänge durch Integration
Beispiel
Wir wollen nun einen Beispiel berechnen. Wir haben eine Kurve, die sei
![]()
Wie du siehst, ist diese Kurve parametrisch; wenn du eine Kurve hast, die durch eine Funktion f in Abhängigkeit von x gegeben ist, kannst du diese mittels
![]()
in eine parametrische Kurve umwandeln.
Das Prinzip der Längenberechnung besteht nun darin, die Länge der Kurve, ähnlich wie bei der Flächenberechnung mit Streifen, mit Strecken anzunähern. Man teilt die Kurve in kleine Teilabschnitte. Jedem Abschnitt kann man jetzt ein Steigungdreieck so einbeschreiben, dass die Hypotenuse die angenäherte Länge des Teilabschnitts ist, also gilt für die angenäherte Länge eines beispielhaften Teilabschnitts
![]()
Rückt man die Teilabschnittspunkte unendlich nahe zusammen, so werden auch die Differenzen in x- und y-Richtung klein. Die Länge der gesamten Kurve für
![]() ist dann also
ist dann also
![]()
Nun setzen wir unsere Werte ein und erhalten als Ergebnis