Lagebeziehung zweier Geraden
Es gibt mehrere Möglichkeiten wie zwei Geraden im Raum zueinander liegen können. Wir zählen diese zunächst einmal auf und erläutern anschließend noch einmal genauer was es mit den verschiedenen Lagebeziehungen auf sich hat und wie man erkennen kann in welcher Beziehung zwei Geraden zueinander stehen.
| Identisch | Zwei Geraden sind identisch, wenn sie genau aufeinander liegen. Jeder Punkt der einen Geraden gehört auch zu der anderen. Es gibt sozusagen unendlich viele Schnittpunkte. |
| Schnittpunkt | Die zwei Geraden schneiden sich an genau einen Punkt, verlaufen aber dann in verschiedene Richtungen. |
| Echt parallel | Die beiden Geraden verlaufen parallel zueinander. Die Richtungsvektoren sind identisch oder linear abhängig. Es gibt kein Schnittpunkt. Der Abstand der Geraden ist an allen Punkten identisch. |
| Windschief | Die zwei Geraden schneiden sich nicht, sind aber auch nicht Parallel. Diese Möglichkeit besteht nur bei Geraden im dreidimensionalen Raum. |
Lagebeziehung zweier Geraden bestimmen
Im Folgenden zeigen wir, wie man überprüft um welche Lagebeziehung es sich bei zwei Geraden handelt. Wir gehen dabei nach diesem Diagramm vor:
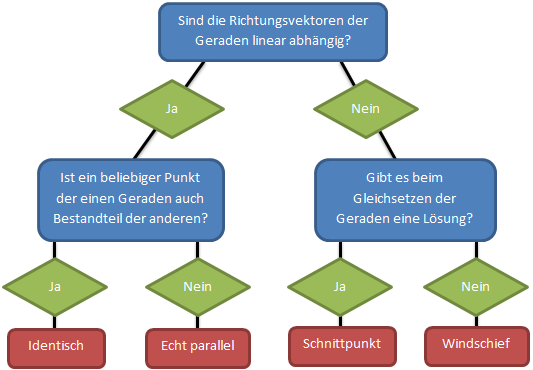
Beispiel 1
Gegeben sind die folgenden beiden Geraden:
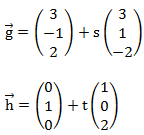
Wir gehen nun Schritt für Schritt durch das Diagramm.
Schritt 1: Sind die Richtungsvektoren der Geraden linear abhängig?
Um dies zu beantworten müssen wir überprüfen, ob der eine Richtungsvektor ein Vielfaches des anderen ist. Hierfür stellen wir folgende Formel auf, die es zu überprüfen gilt:
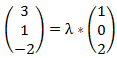
Hiermit überprüfen wir, ob der erste Richtungsvektor ein Vielfaches des zweiten ist. Es ergeben sich folgende Gleichungen:
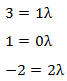
Damit die Vektoren linear abhängig sind, müssten die drei Gleichungen alle mit demselben Lambdawert (λ) lösbar sein. Dies ist nicht der Fall. In der ersten Gleichung müsste Lambda gleich 3 sein. Die zweite Gleichung ist überhaupt nicht lösbar und in der dritten Gleichung müsste Lambda gleich -1 sein.
Die Vektoren sind linear unabhängig.
Schritt 2: Gibt es beim Gleichsetzen der Geraden eine Lösung?
Hierfür müssen wir die beiden Geradengleichungen gleichsetzen:
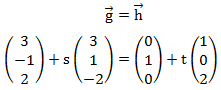
Wir notieren die drei Gleichungen:
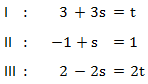
Es handelt sich hierbei um ein lineares Gleichungssystem. Dieses können wir auf unterschiedliche Weise lösen. Wir entscheiden uns für das Einsetzungsverfahren. Dies bietet sich an, da die erste Gleichung bereits nach t umgeformt ist. Außerdem kommt in der zweiten Gleichung nur s vor. Wir formen deshalb die zweite Gleichung nach s um:
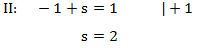
Diese Lösung können wir nun in Gleichung I einsetzen und damit t bestimmen:
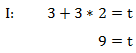
Wir setzen die beiden Lösungen in die dritte Gleichung ein und überprüfen diese:
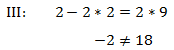
Wir sehen, dass diese Gleichung nicht erfüllt ist.
Es gibt beim Gleichsetzen der beiden Geraden also keine Lösung!
Die beiden Geraden sind damit Windschief.
Beispiel 2
Gegeben sind die folgenden beiden Geraden:
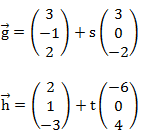
Schritt 1: Sind die Richtungsvektoren der Geraden linear abhängig?
Wir überprüfen, ob der erste Richtungsvektor ein Vielfaches des zweiten ist:
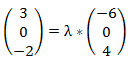
Damit ergeben sich diese Gleichungen:
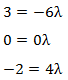
Aus der ersten Gleichung geht hervor:
![]()
Lambda ist damit gleich -0,5. Dies passt auch zu den anderen Gleichungen die damit erfüllt sind.
Die Vektoren sind also linear abhängig.
Schritt 2: Ist ein beliebiger Punkt der einen Geraden auch Bestandteil der anderen?
Wir können uns für die Überprüfung einen beliebigen Punkt auf der ersten Geraden aussuchen und anschließend prüfen ob dieser auch Bestandteil der zweiten Gerade ist. Üblicherweise nimmt man hierfür den Ortsvektor der ersten Gerade, da dieser sicher auf der ersten Geraden liegt.
Wir Überprüfen also ob der Punkt
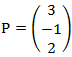
auf der Geraden
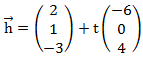
liegt.
Hierfür setzen wir die Gerade mit dem Punkt gleich:
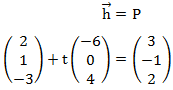
Es ergeben sich wieder drei Gleichungen:
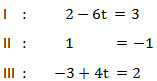
Wir sehen deutlich, dass Gleichung 2 nicht erfüllt werden kann.
Damit gibt es keine Lösung für das Gleichungssystem.
Der Punkt liegt also nicht auf der Geraden.
Die beiden Geraden sind damit parallel.
