Lineare Abhängigkeit 3 Vektoren
Eigenschaften der Vektoren im R3
♦2 Vektoren sind im R3 genau dann linear abhängig, wenn sie parallel sind
♦3 Vektoren sind im R3 genau dann linear abhängig, wenn sie in einer Ebene liegen (dort können sie auch untereinander parallel sein)
♦4 (oder mehr) Vektoren sind im R3 stets linear abhängig
Merke: sind sie koplanar, dann sind sie auch linear abhängig. Zusätzlich sind drei Vektoren allerdings auch linear abhängig, wenn durch Strecken bzw. Stauchen (also durch Verlängern oder Verkürzen der Vektoren) eine Vektorkette gebildet werden kann
Es gibt einige Möglichkeiten um die Lineare Abhängigkeit zu bestimmen. Aber das einfache ist das Determinanten Verfahren, welches wir auch in unseren Beispielen anwenden werden.
Definition Determinante
Eine Determinante ist eine Zahl, die einer quadratischen Matrix zugeordnet ist
♦Die Determinante kann man mit der Sarrus Regel bestimmen ( wird auch Cramersche Regel genannt)
Sarrus Regel ( Formel)
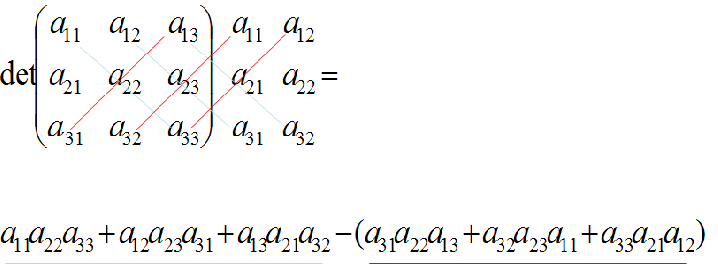
Beispiel
Wir haben folgende 3 Vektoren gegeben
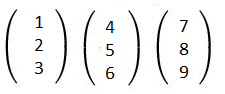
Wir schreiben das ganze nun in einer Matrixform auf
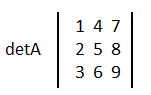
Mit dem Sarrus Regel können wir jetzt die Determinante bestimmen
det(A) = (1*5*9) + ( 4*8*3) + (7*2*6) – ( 3*5*7) – ( 6*8*1) – ( 9*2*4)
⇒ (45 + 96 + 84 )- (105 – 48 – 72)
⇒225 -225
= 0
Da die Determinante gleich Null ist, sind die Vektoren linear Abhängig!
