Lineare Funktionen Einführung

Wenn wir uns an die proportionalen Zuordnungen erinnern ist dies ganz ähnlich. Auch proportionale Zuordnungen kann man als proportionale Funktion bezeichnen. Wir hatten damals die Zuordnung:

y = k • x

Hier kann man einen x-Wert einsetzen und bekommt mithilfe der Funktion den zugehörigen y-Wert. Dies ist natürlich eine relativ einfache Funktion und damit sehr gut geeignet um die Zusammenhänge zu erklären.

Wir setzen in die Funktion nun ein paar Werte ein und erstellen dadurch eine Wertetabelle. Dafür brauchen wir natürlich eine bestimmte Zahl für k. Wir nehmen hier k = 0,5. Unsere Funktion ist also:

y = 0,5 • x

Anschließend erstellen wir die Wertetabelle indem wir einige Werte für x einsetzen. Im Prinzip können wir einen beliebigen Wert für x einsetzen. Da wir die Funktion gleich zeichnen wollen nehmen wir hier die Werte von -5 bis +5.

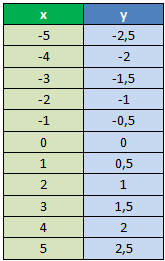
Für die erste Zeile setzt man nun zum Beispiel den x-Wert von -5 in die Funktion ein. Anschließend rechnet man 0,5 • (-5) = -2,5 und schreibt das Ergebnis in die rechte Spalte. Genauso geht man mit den anderen Zeilen vor.

Nachdem man nun diese Wertetabelle hat, kann man die Punkte in ein Koordinatensystem einzeichnen und anschließend mit einem Lineal verbinden.

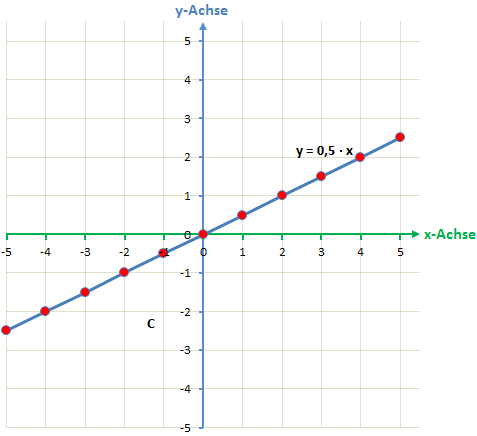
Wir erhalten so eine Funktion wie wir sie auch von den proportionalen Zuordnungen kennen. Diese Funktion ist auch schon eine lineare Funktion. Das einzige was nun noch dazu kommt um alle linearen Funktionen abzudecken ist, dass wir die Funktion nun noch nach oben und unten verschieben können indem wir einen Wert dazu addieren. Eine allgemeine lineare Funktion sieht also folgendermaßen aus:

y = a • x + b 
oder auch
f(x) = a • x + b

Im Allgemeinen kann man beide Schreibweisen benutzen. Das f(x) bedeutet, dass es eine Funktion ist, die von x abhängig ist. f ist der Name der Funktion. Wenn man nur eine Funktion hat, benutzt man meistens f (f steht für „Funktion“). Wenn man mehrere Funktionen hat, sollte man auf jeden Fall die zweite Schreibweise benutzen, da man so die Funktionen gut benennen kann. Die zweite Funktion kann dann zum Beispiel g(x) sein, die dritte h(x) und so weiter.

Das Malzeichen kann man übrigens auch weglassen. Man kann so auch schreiben:

f(x) = ax + b

Die Bedeutung ist genau die Gleiche.