Lineare Gleichungssysteme – Einführung
Lineare Gleichungen haben folgende Form:
y = ax + b
Im Gegensatz zu quadratischen Funktionen ist in ihnen kein Quadrat (hoch 2) vorhanden. Wenn man eine lineare Funktion zeichnet kommt deshalb immer eine Gerade heraus.
Im Kapitel der linearen Gleichungen haben wir bereits gezeigt, wie man mit linearen Funktionen umgeht. Was passiert allerdings wenn wir mehrere lineare Gleichungen haben und diese mehrere Unbekannte haben. Dann haben wir es mit einem linearen Gleichungssystem zu tun. Die Gleichungen gehören dann natürlich zusammen und unser Ziel ist es, Zahlen für die unbekannten Größen zu finden, sodass alle Gleichungen erfüllt sind.
Eine eindeutige Lösung erhält man allerdings nur, wenn man mindestens genauso viele Gleichungen hat wie Variablen. Ist die Variablenanzahl höher als die der Gleichungen, so wird man keine Eindeutige Lösung erhalten. Ist dagegen die Gleichungsanzahl höher als die Variablenanzahl, kann es sein, dass es überhaupt keine Lösung gibt.
Manchmal erhält man keine eindeutige Lösung, obwohl die Variablenanzahl gleich der Anzahl der Gleichungen ist. In diesem Fall sind die Gleichungen linear abhängig. Wir erklären diesen Begriff nachdem wir ein Beispiel betrachtet haben.
Unser Lernvideo zu : Lineare Gleichungssysteme – Einführung
Beispiel Lineares Gleichungssystem
Wir haben folgende Gleichungen:
3z + 2x + y = 0
5x + 4z + y = 4
-3z + 4x -2y = -3
Das Ziel ist es eine Lösung für x, y und z zu finden, sodass alle drei Gleichungen erfüllt sind. In diesem Beispiel wären das:
x = 15
y = 93
z = -41
Verfahren wie man auf diese Werte kommen kann werden wir im Folgenden vorstellen. Wir kontrollieren die Werte indem wir sie in die Gleichungen einsetzen und überprüfen ob der geforderte Wert herauskommt.
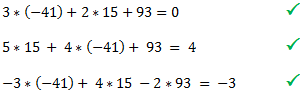
Mit den oben genannten Werten sind also alle drei Gleichungen erfüllt. Die Werte stellen damit eine Lösung des Gleichungssystems dar. In den folgenden Artikeln zeigen wir, wie man auf die Lösung kommen kann.
Lineare Abhängigkeit
Gleichungen sind linear abhängig, wenn man eine Gleichung durch Addition oder Subtraktion der anderen Gleichungen erhält. Ein Beispiel dazu gibt es im Abschnitt „Additionsverfahren“. Es bedeutet, dass die abhängige Gleichung keine neuen Informationen bringt. Wir können sie bei der Lösung des Problems also vernachlässigen. Dies kann natürlich dazu führen, dass ein Gleichungssystem aus 3 Gleichungen und 3 Unbekannten keine eindeutige Lösung hat, wenn die Gleichungen linear abhängig sind.
