Additionsverfahren
Bei dem Additionsverfahren versucht man durch geschicktes addieren oder subtrahieren von Gleichungen Variablen der Gleichungen zu eliminieren. Dadurch erhält man Gleichungen mit weniger Variablen und bei wiederholter Anwendung eine Gleichung mit nur einer Variablen, welche wir dann leicht lösen können.
Unser Lernvideo zu : Additionsverfahren
Beispiel
Wir haben die drei Gleichungen:
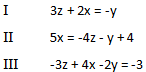
Wir formen die Gleichungen zunächst in eine einheitliche Schreibweise um. Diese sieht folgendermaßen aus:
ax + by + cz = d
Wir schreiben alle Variablen auf die linke Seite des Gleichzeichens und sortieren diese einheitlich. Rechts steht dann also nur noch eine einzelne Zahl.
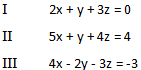
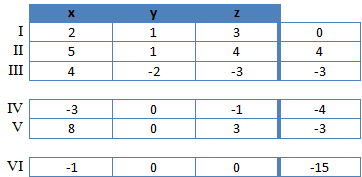
Jetzt können wir die Gleichungen als Gleichungssystem tabellenförmig notieren. Dies erleichtert uns die Arbeit ein wenig.
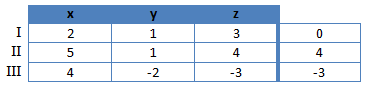
Wir haben so unsere drei Gleichungen sehr übersichtlich notiert. Links befinden sich die Faktoren für die jeweilige Unbekannte. Die dickere Trennlinie stellt das Gleichzeichen dar. Wir versuchen nun, durch geschicktes addieren und subtrahieren der Gleichungen Unbekannte zu eliminieren. Dies machen wir so lange, bis nur noch eine Unbekannte übrig bleibt. Wir beginnen damit die zweite Gleichung von der ersten Gleichung abzuziehen umso das y zu eliminieren.
![]()
Passend dazu müssen wir dann auch in einer weiteren Gleichung das y eliminieren. Wir addieren dafür das Doppelte der ersten Gleichung zu der dritten Gleichung.
![]()
Das komplette Gleichungssystem sieht nun folgendermaßen aus:
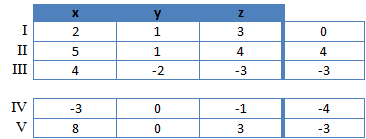
Für die weitere Rechnung dürfen wir nun nur noch die beiden letzten Gleichungen verwenden, da dies die Gleichungen sind in denen kein y mehr vorhanden ist. Wir haben jetzt also noch zwei Unbekannte (x und z) und zwei Gleichungen (IV und V). Wir müssen nun noch eine Unbekannte eliminieren. Wir entscheiden uns für z. Dafür addieren wir das dreifache der Gleichung IV zu der Gleichung V. Wir erhalten:
![]()
Insgesamt sieht es nun also folgendermaßen aus:
Die Gleichung VI hat nun nur noch eine Unbekannte wir können diese also einfach lösen. Die Gleichung VI lautet wie folgt:
![]()
Mit dieser Information können wir uns jetzt weiter vorarbeiten und Gleichung IV oder V lösen. Wir entscheiden uns für Gleichung IV.
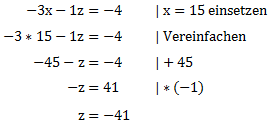
x und z sind uns damit bekannt. Wir benötigen so nur noch y. Wir bekommen y indem wir x und z in eine der ersten drei Gleichungen einsetzen. Wir entscheiden uns für Gleichung I.
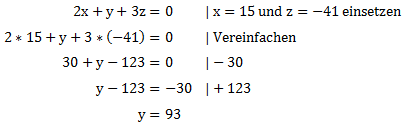
Damit haben wir die Lösung. Wir können diese wie folgt notieren:
![]()
Oder auch:
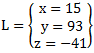
Zur Probe setzen wir die Lösung in die Ausgangsgleichungen ein:
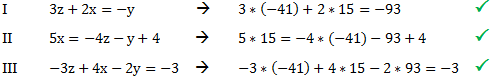
Beispiel mehrere Lösungen
Wir haben die drei Gleichungen:
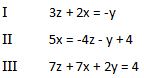
Wir sortieren die Gleichungen, damit wir sie in die Tabelle eintragen können:
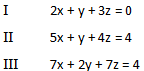
Wir schreiben das Ganze in Tabellenform:
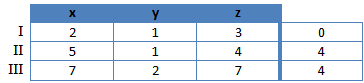
Wir versuchen nun wieder y zu eliminieren und rechnen IV = I – II und V = 2I – III:

Wir erhalten also folgendes komplettes Gleichungssystem:
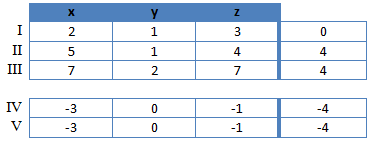
Wir sehen das Gleichung IV und V identisch sind. Dies passiert immer, wenn die Anfangsgleichungen lineare abhängig sind. In diesem Fall ist Gleichung III = I + II. Dadurch ist es, als ob wir nur zwei Ausgangsgleichungen haben. Wir können das Gleichungssystem also nicht eindeutig lösen.
Wir können dennoch eine Lösung angeben. Diese erhalten wir in dem wir Gleichung IV (oder V) nach z umformen:
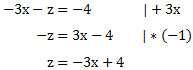
Anschließend müssen wir z = -3x + 4 in eine der ersten drei Gleichungen einsetzen. Wir setzen in die erste ein und formen nach y um:
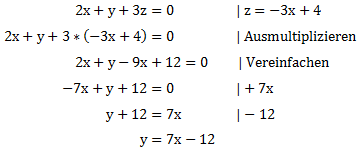
Die Lösung kann also folgendermaßen notiert werden:
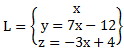
Das bedeutet, dass es unendlich viele Lösungen gibt. Wir können uns einen Wert für x aussuchen und dadurch ergeben sich Werte für y und z. Wir wählen x = 3:
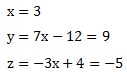
Diese Zahlen stellen eine mögliche Lösung dar. Wir können es überprüfen, indem wir die Zahlen in die Ausgangsgleichungen einsetzen:
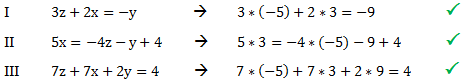
Interessante Fragen und Antworten zu Additionsverfahren
Was ist der Unterschied vom Additionsverfahren und dem Subtraktionsverfahren? |
| Bei zwei Gleichungen wo ebenfalls zwei Unbekannte als gegeben sind, wird vom Linearen Gleichungssystem gesprochen. Das Additionsverfahren ist ein System welches angesetzt wird, um zwei Gleichungen lösen zu können. Ziel ist es also herauszufinden, welche Zahlen gefunden werden müssen, um die beiden vorgegebenen Variablen in der Gleichung aufgehen, also gelöst werden können. Beim Additionsverfahren werden also Gleichungen addiert, damit Variablen wegfallen können. Das Subtraktionsverfahren ist dem bekannten Additionsverfahren zwar relativ ähnlich, besitzt jedoch einen Unterschied. Zunächst wird sich eine beliebige Variable ausgesucht. Beide Gleichungen werden nun auf diese Weise multipliziert, dass genau vor dieser Variable nicht nur die gleiche Zahl sondern auch das gleiche Vorzeichen steht. Beide Gleichungen werde schließlich voneinander abgezogen, so dass nun aufgelöst werden kann. |
Wie funktionieren die 3 Lösungsverfahren Gleichsetzungsverfahren, Einsetzungsverfahren, Additionsverfahren? |
| Hat man zwei Gleichungen mit genau zwei Unbekannten, bietet sich das Gleichsetzungsverfahren an. Hierzu werden beide Gleichungen nach der gleichen Variable umgeformt. Das heißt, dass diese variable alleine hinter dem Gleichzeichen in der Gleichung steht. Nun können beide Gleichungen in eine Gleichung eingesetzt werden. Im Anschluss ist es nun möglich, nach der zweiten Unbekannten aufzulösen, so dass diese ermittelt werden kann.Das Einsetzungsverfahren ist eine Sonderform des Gleichsetzungsverfahren. Auch hier sehen wir uns zwei Gleichungen mit jeweils zwei Unbekannten gegenüber. Im Gegensatz zum Gleichsetzungsverfahren lösen wir jedoch nur eine Gleichung nach einer Unbekannten auf. Diese Unbekannte ersetzen wir im Anschluss in der zweiten Gleichung durch das, was auf der anderen Seite des Gleichheitszeichens übrig bleibt. Die zweite Gleichung kann nun nach der verbliebenen Unbekannten aufgelöst werden.
Das Additionsverfahren kann bei mehreren Gleichungen angewendet werden, die nur aus Additionen bzw. Subtraktionen bestehen. Durch das gleichnamig machen jeweils einer Variable kann diese durch Addition (oder Subtraktion) der Gleichungen voneinander eliminiert werden. Das gleichnamig machen geschieht, indem die Gleichungen jeweils mit einem Faktor multipliziert werden, so dass die ausgesuchte Variable in den beiden verschiedenen Gleichungen den gleichen Wert erhält, allerdings mit unterschiedlichen Vorzeichen. Anschließend fällt diese Variable durch Addition weg. Dieser Vorgang lässt sich wiederholen, bis nur noch eine Variable übrig bleibt, nach welcher dann aufgelöst werden kann. |
Wie funktioniert das Additionsverfahren mit 2 bzw 3 Variablen? |
| Grundsätzlich sind lineare Gleichungssysteme nur dann eindeutig lösbar, wenn sie aus mindestens so vielen Gleichungen wie Variablen bestehen. Liegt das Gleichungssystem nicht in Dreiecksgestalt vor, aus der man bereits eine Variable bestimmen könnte, muss man durch Äquivalenzumformungen und Addition oder Subtraktion von Gleichungen versuchen, es in die Dreiecksform zu überführen. Ziel ist es also, dass man eine Gleichung mit nur einer Variablen erhält und bei insgesamt zwei Variablen dann noch eine weitere, die diese beiden enthält, bei drei Variablen noch zwei weitere mit jeweils zwei bzw. drei Variablen. Dann kann man die mit nur einer Variablen nach genau dieser Variablen auflösen und durch sukzessives Einsetzen in die andere(n) Gleichungen auch die übrigen Variablen ausrechnen. |
