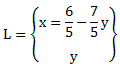Einsetzungsverfahren
Das Einsetzungsverfahren ist wie das Gleichsetzungsverfahren nützlich, um aus zwei Gleichungen mit zwei verschiedenen Variablen eine einzelne Gleichung zu formen, die nur noch eine Variable enthält. Daraus kann dann eine exakte Lösung berechnet werden. Ziel ist es den möglichen Schnittpunkt der beiden Gleichungen zu berechnen. Dieser hat immer zwei Koordinaten: Schnittpunkt S (x/y).
Erklärung des Verfahrens
Gegeben sind zwei Gleichungen mit insgesamt zwei verschiedenen Variablen z.B. x & y. Zunächst wird eine der beiden Gleichungen nach einer beliebigen Variablen umgeformt, so dass dann dort steht: x = … oder y = …
Nun können wir die Variable in der anderen Gleichung ersetzen und fügen ein. Somit haben wir nun eine Gleichung mit nur einer Unbekannten. Diese können wir, wie erlernt auflösen und danach auch die zweite Variable berechnen und erhalten ein eindeutiges Ergebnis.
Beispiel 1
Wir haben folgende Ausgangsgleichungen:
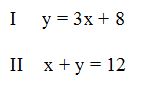
Da die erste Gleichung bereits nach y umgeformt ist, setzen wir sie nun in die zweite Gleichung den Wert für y ein:
![]()
Nun haben wir anstelle der Variablen y den Wert 3x + 8 eingesetzt und somit nur noch eine Unbekannte.
Als nächsten formen wir die Gleichung nach x um. Dazu müssen wir zunächst die Klammer auflösen:

Nun haben wir das Ergebnis x = 4 erhalten. Das zeigt uns an, das unser Lösungswert im Koordinatensystem auf der X-Achse bei 4 liegt. Um den Punkt eindeutig zu bestimmen, benötigen wir nun noch die Y-Koordinate. Dazu setzen wir unseren eben errechneten X-Wert in eine der Ausgangsgleichungen ein. Dabei ist es egal welche es ist, denn es kommt jedesmal der gleiche Wert heraus.
Wir setzen den X- Wert in die Gleichung I ein, da diese bereits nach y aufgelöst ist und rechnen aus:
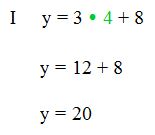
Für y erhalten wir den Wert 20.
Somit wissen wir, dass unser gesuchter Punkt auf der Y-Achse den Wert 20 hat und somit erhalten wir das eindeutige Ergebnis: S (4/20)
Beispiel 2
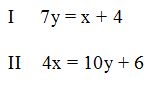
1. Schritt: Wir lösen eine beliebige Gleichung nach einer Variablen auf. In diesem Fall bietet es sich an Gleichung I nach x aufzulösen, da diese ohne Vervielfachungswert auftritt:
2. Schritt: Nun das Ergebnis in die Gleichung II einsetzen:
![]()
3. Schritt: Nun haben wir eine Gleichung mit nur einer Variablen. Nach dieser wird nun aufgelöst:

4 Schritt: Errechneten Y-Wert in eine beliebige Ausgangsgleichung einsetzen:
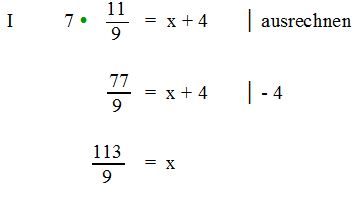
Somit haben wir den Schnittpunkt der beiden Gleichungen ermittelt:
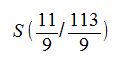
Unser Lernvideo zu : Einsetzungsverfahren
Beispiel mit unendlich vielen Lösungen
Es kommt vor, dass wir ein allgemeingültiges Ergebnis erhalten. Z. B.: 3 = 3
Das bedeutet, dass die Gleichungen unendlich viele Lösungen haben, da die Geraden identisch sind.
Beispiel
Wir haben diese beiden Gleichungen:
![]()
Wenn wir nun wie eben vorgehen und die erste Gleichung nach x umformen, erhalten wir folgendes Ergebnis:
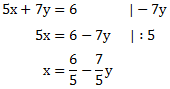
Das Ergebnis setzen wir nun in die zweite Gleichung ein:
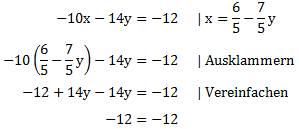
Die Gleichung ist also immer erfüllt, egal welchen Wert man für y einsetzt. Dies bedeutet, dass die beiden Gleichungen linear abhängig sind. Die zweite Gleichung entsteht wenn man die erste Gleichung mit -2 multipliziert. Wir können die Lösungsmenge wie folgt angeben. Es gibt unendliche viele Lösungen, da man y frei wählen kann. Der x-Wert hängt dann von dem gewählten y-Wert ab.